
【题目】设函数g(x)=sinωx(ω>0)向左平移![]() 个单位长度得到函数f(x),已知f(x)在[0,2π]上有且只有5个零点,则下列结论正确的是( )
个单位长度得到函数f(x),已知f(x)在[0,2π]上有且只有5个零点,则下列结论正确的是( )
A.f(x)的图象关于直线![]() 对称
对称
B.f(x)在(0,2π)上有且只有3个极大值点,f(x)在(0,2π)上有且只有2个极小值点
C.f(x)在![]() 上单调递增
上单调递增
D.ω的取值范围是[![]() )
)
科目:高中数学 来源: 题型:
【题目】垃圾分类是对垃圾进行有效处置的一种科学管理方法,为了了解居民对垃圾分类的知晓率和参与率,引导居民积极行动,科学地进行垃圾分类,某小区随机抽取年龄在区间![]() 上的50人进行调研,统计出年龄频数分布及了解垃圾分类的人数如下表:
上的50人进行调研,统计出年龄频数分布及了解垃圾分类的人数如下表:
年龄 |
|
|
|
|
|
|
频数 | 5 | 10 | 10 | 15 | 5 | 5 |
了解 | 4 | 5 | 8 | 12 | 2 | 1 |
(1)填写下面2×2列联表,并判断能否在犯错误的概率不超过0.01的前提下认为以65岁为分界点居民对了解垃圾分类的有关知识有差异;
年龄低于65岁的人数 | 年龄不低于65岁的人数 | 合计 | |
了解 |
|
| |
不了解 |
|
| |
合计 |
(2)若对年龄在![]() ,
,![]() 的被调研人中各随机选取2人进行深入调研,记选中的4人中不了解垃圾分类的人数为X,求随机变量X的分布列和数学期望
的被调研人中各随机选取2人进行深入调研,记选中的4人中不了解垃圾分类的人数为X,求随机变量X的分布列和数学期望
参考公式和数据
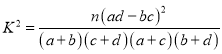 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年双十一落下帷幕,天猫交易额定格在268(单位:十亿元)人民币(下同),再创新高,比去年218(十亿元)多了50(十亿元).这些数字的背后,除了是消费者买买买的表现,更是购物车里中国新消费的奇迹,为了研究历年销售额的变化趋势,一机构统计了2010年到2019年天猫双十一的销售额数据y(单位:十亿元),绘制如表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
销售额y | 0.9 | 8.7 | 22.4 | 41 | 65 | 94 | 132.5 | 172.5 | 218 | 268 |
根据以上数据绘制散点图,如图所示
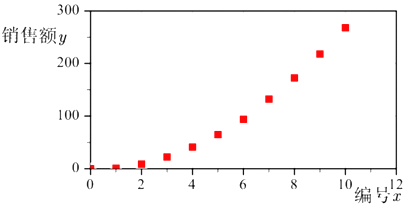
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为销售额
哪一个适宜作为销售额![]() 关于
关于![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及如表中的数据,建立![]() 关于
关于![]() 的回归方程,并预测2020年天猫双十一销售额;(注:数据保留小数点后一位)
的回归方程,并预测2020年天猫双十一销售额;(注:数据保留小数点后一位)
(3)把销售超过100(十亿元)的年份叫“畅销年”,把销售额超过200(十亿元)的年份叫“狂欢年”,从2010年到2019年这十年的“畅销年”中任取2个,求至少取到一个“狂欢年”的概率.
参考数据:![]()
|
|
|
|
|
|
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别
的斜率和截距的最小二乘估计公式分别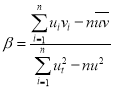 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的圾坐标方
).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的圾坐标方![]() ,且直线l与曲线C相交于A,B两点.
,且直线l与曲线C相交于A,B两点.
(1)求曲线C的普通方程和l的直角坐标方程;
(2)若![]() ,点
,点![]() 满足
满足![]() ,求此时r的值.
,求此时r的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,将其左、右焦点和短轴的两个端点顺次连接得到一个面积为
,将其左、右焦点和短轴的两个端点顺次连接得到一个面积为![]() 的正方形.
的正方形.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点(均不在
两点(均不在![]() 轴上),点
轴上),点![]() ,若直线
,若直线![]() 、
、![]() 、
、![]() 的斜率成等比数列,且
的斜率成等比数列,且![]() 的面积为
的面积为![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了提高生产效率,对生产设备进行了技术改造,为了对比技术改造后的效果,采集了技术改造前后各20次连续正常运行的时间长度(单位:天)数据,整理如下:
改造前:19,31,22,26,34,15,22,25,40,35,18,16,28,23,34,15,26,20,24,21
改造后:32,29,41,18,26,33,42,34,37,39,33,22,42,35,43,27,41,37,38,36
(1)完成下面的列联表,并判断能否有99%的把握认为技术改造前后的连续正常运行时间有差异?
超过30 | 不超过30 | |
改造前 | ||
改造后 |
(2)工厂的生产设备的运行需要进行维护,工厂对生产设备的生产维护费用包括正常维护费,保障维护费两种.对生产设备设定维护周期为T天(即从开工运行到第kT天,k∈N*)进行维护.生产设备在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产设备能连续运行,则只产生一次正常维护费,而不会产生保障维护费;若生产设备不能连续运行,则除产生一次正常维护费外,还产生保障维护费.经测算,正常维护费为0.5万元/次;保障维护费第一次为0.2万元/周期,此后每增加一次则保障维护费增加0.2万元.现制定生产设备一个生产周期(以120天计)内的维护方案:T=30,k=1,2,3,4.以生产设备在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及均值.
附: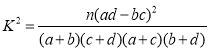
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调査了部分市民(问卷调査表如下表所示),并根据调查结果绘制了尚不完整的统计图表(如下图)

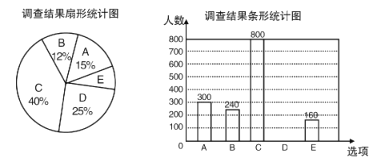
由两个统计图表可以求得,选择D选项的人数和扇形统计图中E的圆心角度数分别为( )
A.500,28.8°B.250,28.6°C.500,28.6°D.250,28.8°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C方程为![]() ,椭圆中心在原点,焦点在x轴上.
,椭圆中心在原点,焦点在x轴上.
(1)证明圆C恒过一定点M,并求此定点M的坐标;
(2)判断直线![]() 与圆C的位置关系,并证明你的结论;
与圆C的位置关系,并证明你的结论;
(3)当![]() 时,圆C与椭圆的左准线相切,且椭圆过(1)中的点M,求此时椭圆方程;在x轴上是否存在两定点A,B使得对椭圆上任意一点Q(异于长轴端点),直线
时,圆C与椭圆的左准线相切,且椭圆过(1)中的点M,求此时椭圆方程;在x轴上是否存在两定点A,B使得对椭圆上任意一点Q(异于长轴端点),直线![]() ,
,![]() 的斜率之积为定值?若存在,求出A,B坐标;若不存在,请说明理由.
的斜率之积为定值?若存在,求出A,B坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在![]() 上任意一点
上任意一点![]() 处的切线
处的切线![]() 为
为![]() ,若过右焦点
,若过右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,已知在点
两点,已知在点![]() 处切线相交于
处切线相交于![]() .
.
(Ⅰ)求![]() 点的轨迹方程;
点的轨迹方程;
(Ⅱ)①若过点![]() 且与直线
且与直线![]() 垂直的直线(斜率存在且不为零)交椭圆
垂直的直线(斜率存在且不为零)交椭圆![]() 于
于![]() 两点,证明
两点,证明![]() 为定值.
为定值.
②四边形![]() 的面积是否有最小值,若有请求出最小值;若没有请说明理由.
的面积是否有最小值,若有请求出最小值;若没有请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com