
已知函数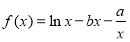 (
(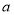 、
、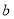 为常数),在
为常数),在 时取得极值.
时取得极值.
(1)求实数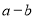 的值;
的值;
(2)当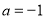 时,求函数
时,求函数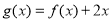 的最小值;
的最小值;
(3)当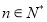 时,试比较
时,试比较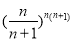 与
与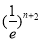 的大小并证明.
的大小并证明.
(1)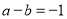 ;(2)
;(2)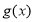 取最小值
取最小值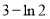 ;(3)
;(3)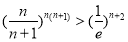 .
.
【解析】
试题分析:(1)因为函数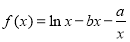 (
(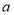 、
、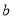 为常数),在
为常数),在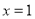 时取得极值,故
时取得极值,故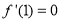 ,因此,先对函数
,因此,先对函数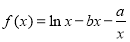 求导得,
求导得,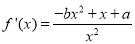 ,由
,由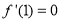 可得实数
可得实数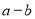 的值;(2)当
的值;(2)当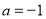 时,求函数
时,求函数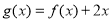 的最小值,当
的最小值,当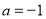 时,由
时,由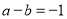 得
得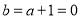 ,代入得
,代入得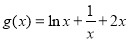
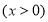 ,对
,对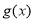 求导,判断单调性,即可得函数
求导,判断单调性,即可得函数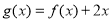 的最小值;(3)比较
的最小值;(3)比较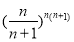 与
与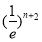 的大小,直接比较不好比较,可比较对数的大小即
的大小,直接比较不好比较,可比较对数的大小即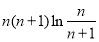 与
与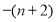 ,两式作差得
,两式作差得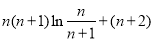 ,只需判断它的符号,即判断
,只需判断它的符号,即判断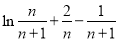 的符号,即判断
的符号,即判断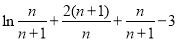 的符号,可构造函数
的符号,可构造函数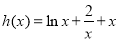 ,证明
,证明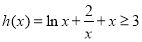 即可.
即可.
试题解析:(1)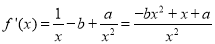
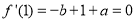
∴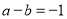 (3分)
(3分)
(2)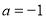 时
时 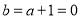
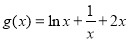
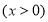 ,
,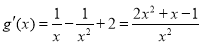
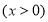
∴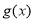 在
在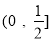 上单调递减,在
上单调递减,在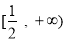 上单调递增 (6分)
上单调递增 (6分)
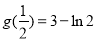
∴当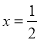 时,
时,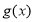 取最小值
取最小值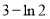 (8分)
(8分)
(3)令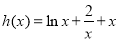
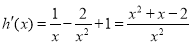
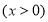 ,∴
,∴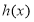 在
在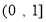 上单调递减,在
上单调递减,在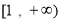 上单调递增
上单调递增 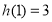 ,∴
,∴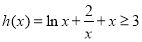 当且仅当
当且仅当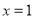 时取最小值
时取最小值
∵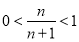 ∴
∴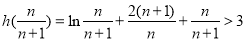
∴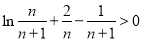 ∴
∴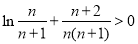
∴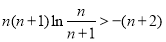 ∴
∴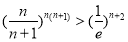 (14分)
(14分)
考点:函数的极值,函数的最值,比较大小,函数的单调性.


科目:高中数学 来源:2013-2014学年江西省鹰潭市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
在长为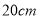 的线段
的线段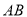 上任取一点
上任取一点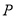 ,并且以线段
,并且以线段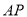 为边作正三角形,则这个正三角形
为边作正三角形,则这个正三角形
的面积介于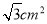 与
与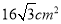 之间的概率为( )
之间的概率为( )
A.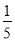 B.
B.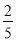 C.
C.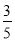 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第二次联考文科数学试卷(解析版) 题型:选择题
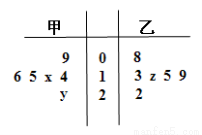
甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,其中甲成绩的中位数为15,极差为12;乙成绩的众数为13,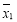 ,
,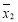 分别表示甲乙两名运动员这项测试成绩的平均数,
分别表示甲乙两名运动员这项测试成绩的平均数,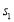 ,
,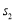 分别表示甲乙两名运动员这项测试成绩的标准差,则有 ( )
分别表示甲乙两名运动员这项测试成绩的标准差,则有 ( )
A.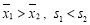 B.
B.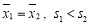
C.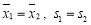 D.
D.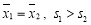
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第一次联考理科数学试卷(解析版) 题型:填空题
下图给出了一个程序框图,其作用是输入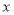 的值,输出相应的
的值,输出相应的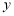 值.若要使输入的
值.若要使输入的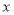 值与输出的
值与输出的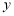 值相等,则这样的
值相等,则这样的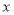 值有__________个.
值有__________个.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第一次联考文科数学试卷(解析版) 题型:解答题
在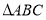 中,角
中,角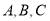 所对的边分别为
所对的边分别为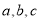 ,函数
,函数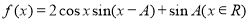 在
在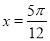 处取得最大值.
处取得最大值.
(1)求角A的大小.
(2)若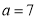 且
且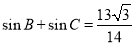 ,求
,求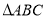 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第一次联考文科数学试卷(解析版) 题型:选择题
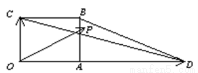
如图,四边形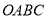 是边长为1的正方形,
是边长为1的正方形,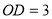 ,点
,点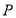 为
为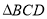 内(含边界)的动点,设
内(含边界)的动点,设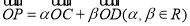 ,则
,则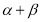 的最大值等于( )
的最大值等于( )
A.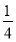 B.1 C.
B.1 C.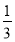 D.
D.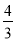
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省宜春市高三考前模拟理科数学试卷(解析版) 题型:填空题
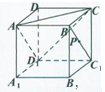
如图,正方体ABCD-A1B1C1D1中,点P是直线BC1的动点,则下列四个命题:
①三棱锥A-D1PC的体积不变;
②直线AP与平面ACD1所成角的大小不变;
③二面角P-AD1-C的大小不变:
其中正确的命题有____ .(把所有正确命题的编号填在横线上)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省南昌市高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
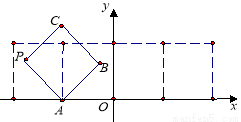
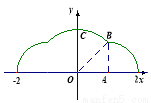
如图放置的边长为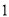 的正方形
的正方形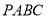 沿
沿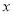 轴滚动,点
轴滚动,点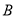 恰好经过原点.设顶点
恰好经过原点.设顶点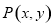 的轨迹方程是
的轨迹方程是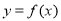 ,则对函数
,则对函数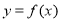 有下列判断:①函数
有下列判断:①函数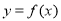 是偶函数;②对任意的
是偶函数;②对任意的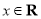 ,都有
,都有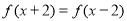 ;③函数
;③函数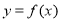 在区间
在区间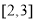 上单调递减;④
上单调递减;④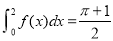 .其中判断正确的序号是 .
.其中判断正确的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com