已知一次函数f(x)是增函数且满足f(f(x))=4x-3.
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)若不等式f(x)<m对于一切x∈[-2,2]恒成立,求实数m的取值范围.
解:(1)由题意可设f(x)=ax+b(a>0).
由f(f(x))=4x-3,得:a(ax+b)+b=4x-3,
即a
2x+ab+b=4x-3,所以,
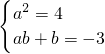
,
解得:
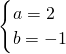
或
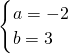
,
因为a>0,所以a=2,b=-1.
所以f(x)=2x-1;
(2)由f(x)<m,得m>2x-1.
不等式f(x)<m对于一切x∈[-2,2]恒成立,
即为m>2x-1对于一切x∈[-2,2]恒成立,
因为函数f(x)=2x-1在[-2,2]上为增函数,所以f
max(x)=f(2)=3.
所以m>3.
所以,不等式f(x)<m对于一切x∈[-2,2]恒成立的实数m的取值范围(3,+∞).
分析:(1)根据一次函数f(x)是增函数,设出一次函数的表达式,代入f(f(x))=4x-3,利用系数相等可求一次函数解析式;
(2)根据(1)中求出的函数是增函数,直接求出f(x)在[-2,2]上的最大值,则实数m的取值范围可求.
点评:本题考查了一次函数的图象和性质,考查了利用代入法求函数解析式,本题的(2)实则是分离变量的解题思想,此题是基础题.

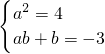 ,
,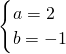 或
或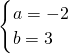 ,
,
