
【题目】设集合M={m|m∈Z,且|m|≤2018},M的子集S满足:对S中任意3个元素a,b,c(不必不同),都有a+b+c≠0.求集合S的元素个数的最大值.
【答案】20
【解析】
集合S的元素个数的最大值为2018.
令S={s|1≤s≤2018,s∈Z},显然集合S符合要求,且|S|=2018.
另一方面,设S是满足题设条件的集合,显然![]() (否则0+0+0=0).设S中的所有正整数构成集合A,S中的所有负整数构成集合B.
(否则0+0+0=0).设S中的所有正整数构成集合A,S中的所有负整数构成集合B.
若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() .
.
下面考虑A、B非空的情形.
对于集合X, Y,记![]() ,
,![]() .
.
由题设可知,![]() (否则,设x0∈(A+B)∩(-S),则存在a∈A,b∈B,-c∈-S,使得a+b=x0,-c=x0.于是,存在a∈S,b∈S,使得a+b+c=0).且A+B∈{x|x∈Z,且|x|<2017}(事实上,A中元素≤2018,B中元素≤-1,于是A+B中元素≤2017;同理,A+B中元素≥-1027.).
(否则,设x0∈(A+B)∩(-S),则存在a∈A,b∈B,-c∈-S,使得a+b=x0,-c=x0.于是,存在a∈S,b∈S,使得a+b+c=0).且A+B∈{x|x∈Z,且|x|<2017}(事实上,A中元素≤2018,B中元素≤-1,于是A+B中元素≤2017;同理,A+B中元素≥-1027.).
设集合A中元素为a1,a2,…,ak,集合B中元素为b1,b2,…,bl,且a1<a2<…<ak,b1<b2<…<bl.
∵a1+b1<a2+b1<a3+b1<…<ak+bl <ak+b2<…< ak+bl.
∴A+B中至少有k+l-1个元素,即|A+B|≥k+l-1=|S|-1.
结合![]() ,
,![]() ,且
,且![]() ,可得
,可得![]() ,4037=|M|≥|A+B|+|-S|=|A+B|+|S|≥|S|-1+|S|.
,4037=|M|≥|A+B|+|-S|=|A+B|+|S|≥|S|-1+|S|.
∴|S|≤2019.
若|S|=2019,则|A+B|+|-S|=4037=|M|.
∴(A+B)∪(-S)=M.
又由![]() ,
,![]() ,知2018∈S,-2018∈S.
,知2018∈S,-2018∈S.
∴对于k=1,2,3,…,1009,k与2018-k中至少有一个不属于S,-k与-2018+k中也至少有一个不属于S.因此,|A|≤1009,|B|≤1009.
∴2019=|S|=|A|+|5|≤1009+1009=2018,矛盾.
因此,![]() .
.
综上可得,![]() .
.
综上所述,集合S的元素个数的最大值为2018.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,左、右焦点分别为F1,F2,且|F1F2|=2,点(1, ![]() )在椭圆C上。
)在椭圆C上。
(1)求椭圆C的方程;
(2)过F1的直线l与椭圆C相交于A,B两点,且△AF2B的面积为![]() ,求以F2为圆心且与直线l相切的圆的方程。
,求以F2为圆心且与直线l相切的圆的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心在坐标原点,且与直线
的圆心在坐标原点,且与直线![]() 相切.
相切.
(1)求直线![]() 被圆
被圆![]() 所截得的弦
所截得的弦![]() 的长;
的长;
(2)过点![]() 作两条与圆
作两条与圆![]() 相切的直线,切点分别为
相切的直线,切点分别为![]() 求直线
求直线![]() 的方程;
的方程;
(3)若与直线![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() 为钝角,求直线
为钝角,求直线![]() 在
在![]() 轴上的截距的取值范围.
轴上的截距的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△DEF三边所在的直线分别为l1:x=-2,l2:x+![]() y-4=0,l3:x-
y-4=0,l3:x-![]() y-4=0,⊙C为△DEF的内切圆.
y-4=0,⊙C为△DEF的内切圆.
(1)求⊙C的方程;
(2)设⊙C与x轴交于A、B两点,点P在⊙C内,且满足![]() .记直线PA、PB的斜率分别为k1、k2,求k1 k2的取值范围.
.记直线PA、PB的斜率分别为k1、k2,求k1 k2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知P点到两定点D(﹣2,0),E(2,0)连线斜率之积为- ![]() .
.
(1)求证:动点P恒在一个定椭圆C上运动;
(2)过 ![]() 的直线交椭圆C于A,B两点,过O的直线交椭圆C于M,N两点,若直线AB与直线MN斜率之和为零,求证:直线AM与直线BN斜率之和为定值.
的直线交椭圆C于A,B两点,过O的直线交椭圆C于M,N两点,若直线AB与直线MN斜率之和为零,求证:直线AM与直线BN斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC为等边三角形,AE=1,BD=2,CD与平面ABCDE所成角的正弦值为 ![]() .
. 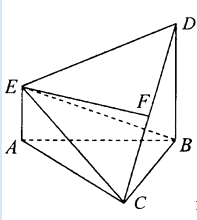
(1)若F是线段CD的中点,证明:EF⊥平面DBC;
(2)求二面角D﹣EC﹣B的平面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com