有形状、大小都相同的6只球放在A,B两个口袋中,其中A口袋中有1只白球和2只红球,B口袋中有2个白球和1只红球.
(1)从A,B口袋中各一次性摸出两只球,共得四只球,记其中红球的只数为X,求:P(X=1),P(X=2).
(2)把A,B口袋中的球全放到C口袋中,从C口袋中有放回的摸出3只球,记摸到红球的个数为Y,求Y的概率分布及数学期望E(Y).
解:(I)由题意知本题是一个等可能事件的概率,
P(X=1)=
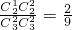
,
P(X=2)=
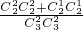
=

.
(II)由题意知变量的可能取值是0,1,2,3
P(Y=0)=
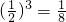
P(Y=1)=
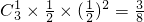
P(Y=2)=
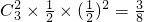
P(Y=3)=

∴Y的分布列是
∴EY=
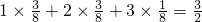
分析:(I)本题是一个等可能事件的概率,要求P(X=1)和P(X=2)的结果,写出试验发生包含的事件数和满足条件的事件数.
(II)由题意知变量的可能取值是0,1,2,3,结合变量对应的事件和独立重复试验的概率公式,写出变量的概率,写出分布列和期望值.
点评:本题考查离散型随机变量的分布列和期望,本题解题的关键是看清题目中涉及到变量对应的事件,看出符合的规律.

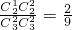 ,
,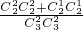 =
= .
.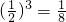
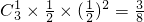
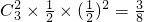





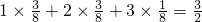


 期末集结号系列答案
期末集结号系列答案