
【题目】对于在区间[a,b]上有意义的两个函数f(x)和g(x),如果对于任意x∈[a,b]均有|f(x)﹣g(x)|≤1成立,则称函数f(x)和g(x)在区间[a,b]上是接近的.若f(x)=log2(ax+1)与g(x)=log2x在区[1,2]上是接近的,则实数a的取值范围是( )
A.[0,1]
B.[2,3]
C.[0,2)
D.(1,4)
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】设全集为R,集合A=(﹣∞,﹣1)∪(3,+∞),记函数f(x)= ![]() 的定义域为集合B
的定义域为集合B
(1)分别求A∩B,A∩RB;
(2)设集合C={x|a+3<x<4a﹣3},若B∩C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,
点, ![]() 为弦
为弦![]() 的中点,直线
的中点,直线![]() 分别与直线
分别与直线![]() 和直线
和直线![]() 交于
交于![]() 两点.
两点.
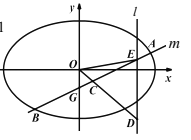
(1)求直线![]() 的斜率和直线
的斜率和直线![]() 的斜率之积;
的斜率之积;
(2)分别记![]() 和
和![]() 的面积为
的面积为![]() ,是否存在正数
,是否存在正数![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的取值;若不存在,说明理由.
的取值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个顶点A、B、C及平面内一点P满足 ![]() +
+ ![]() =
= ![]() ,下列结论中正确的是( )
,下列结论中正确的是( )
A.P在△ABC的内部
B.P在△ABC的边AB上
C.P在AB边所在直线上
D.P在△ABC的外部
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx﹣x2+1.
(Ⅰ)若曲线y=f(x)在x=1处的切线方程为4x﹣y+b=0,求实数a和b的值;
(Ⅱ)讨论函数f(x)的单调性;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AA1= ![]() ,AB=1,AD=2,E为BC的中点,点M为棱AA1的中点.
,AB=1,AD=2,E为BC的中点,点M为棱AA1的中点. 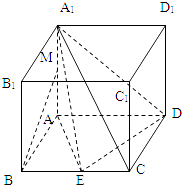
(1)证明:DE⊥平面A1AE;
(2)证明:BM∥平面A1ED.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中,已知PA=PB=PC=AC=4,BC= ![]() AB=2
AB=2 ![]() ,O为AC中点.
,O为AC中点. 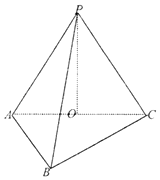
(1)求证:PO⊥平面ABC;
(2)求异面直线AB与PC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+mx+n(m、n∈R)的两个零点分别在(0,1)与(1,2)内,则(m+1)2+(n﹣2)2的取值范围是( )
A.![]()
B.![]()
C.[2,5]
D.(2,5)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱柱ABCD﹣A1B1C1D1中,底面ABCD是边长为3的正方形,侧棱AA1长为4,且AA1与A1B1 , A1D1的夹角都是60°,则AC1的长等于( ) 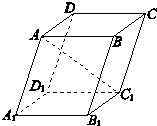
A.10
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com