练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆：的短轴端点为，，点是椭圆上的动点，且不与，重合，点满足，.

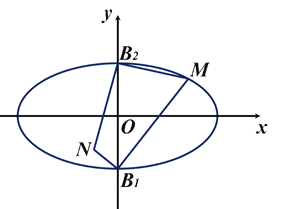
    （Ⅰ）求动点的轨迹方程；

    （Ⅱ）求四边形面积的最大值.

    【答案】（Ⅰ）；（Ⅱ）.

    【解析】

    （Ⅰ）设，，结合垂直关系设出两直线的方程，相乘即可得到动点的轨迹方程；

    （Ⅱ）利用根与系数的关系表示四边形面积，转求函数最值即可.

    （Ⅰ）法一：设，，

    直线

    直线

    得

    又，

    ，

    整理得点的轨迹方程为

    法二：设，，

    直线

    直线

    由,解得：，又，

    故，代入得.

    点的轨迹方程为

    法三：设直线，则直线

    直线与椭圆的交点的坐标为.

    则直线的斜率为.

    直线

    由 解得:点的轨迹方程为：

    （Ⅱ）法一：设，由（Ⅰ）法二得：

    四边形的面积，

    ，当时，的最大值为.

    法二：由（Ⅰ）法三得：四边形的面积

    当且仅当时，取得最大值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： (a>b>0)的一个顶点为A(2,0)，离心率为.直线y＝k(x－1)与椭圆C交于不同的两点M，N.

    (1)求椭圆C的方程；

    (2)当△AMN的面积为时，求k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业甲,乙两个研发小组,他们研发新产品成功的概率分别为和,现安排甲组研发新产品,乙组研发新产品.设甲,乙两组的研发是相互独立的.

    (1)求至少有一种新产品研发成功的概率;

    (2)若新产品研发成功,预计企业可获得万元,若新产品研发成功,预计企业可获得利润万元,求该企业可获得利润的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，曲线由部分椭圆：和部分抛物线：连接而成，与的公共点为，，其中所在椭圆的离心率为.

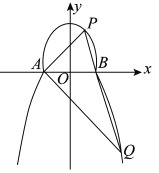
    （Ⅰ）求，的值；

    （Ⅱ）过点的直线与，分别交于点，（，，，中任意两点均不重合），若，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“科技引领，布局未来”科技研发是企业发展的驱动力量。年，某企业连续年累计研发投入搭亿元，我们将研发投入与经营投入的比值记为研发投入占营收比，这年间的研发投入（单位：十亿元）用右图中的折现图表示，根据折线图和条形图，下列结论错误的使（ ）

    A. 年至年研发投入占营收比增量相比年至年增量大

    B. 年至年研发投入增量相比年至年增量小

    C. 该企业连续年研发投入逐年增加

    D. 该企业来连续年来研发投入占营收比逐年增加

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线的倾斜角为，且经过点．以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，直线，从原点O作射线交于点M，点N为射线OM上的点，满足，记点N的轨迹为曲线C．

    （Ⅰ）求出直线的参数方程和曲线C的直角坐标方程；

    （Ⅱ）设直线与曲线C交于P，Q两点，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：的短轴端点为，，点是椭圆上的动点，且不与，重合，点满足，.

    （Ⅰ）求动点的轨迹方程；

    （Ⅱ）求四边形面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】社区服务是高中学生社会实践活动的一个重要内容，汉中某中学随机抽取了100名男生、100名女生，了解他们一年参加社区服务的时间，按，，，，（单位：小时）进行统计，得出男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.

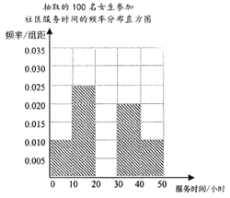
    （1）完善男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.

    抽取的100名男生参加社区服务时间的频率分布表

    社区服务时间

    人数

    频率

    0.05

    20

    0.35

    30

    合计

    100

    1

    学生社区服务时间合格与性别的列联表

    不合格的人数

    合格的人数

    男

    女

    （2）按高中综合素质评价的要求，高中学生每年参加社区服务的时间不少于20个小时才为合格，根据上面的统计图表，完成抽取的这200名学生参加社区服务时间合格与性别的列联表，并判断是否有以上的把握认为参加社区服务时间达到合格程度与性别有关，并说明理由.

    （3）用以上这200名学生参加社区服务的时间估计全市9万名高中学生参加社区服务时间的情况，并以频率作为概率.

    （i）求全市高中学生参加社区服务时间不少于30个小时的人数.

    （ⅱ）对我市高中生参加社区服务的情况进行评价.

    参考公式

    0.150

    0.100

    0.050

    0.025

    0.010

    0.002

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    （，其）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某个公园有个池塘，其形状为直角△ABC，∠C=90°，AB=2百米，BC=1百米．

    (1)现在准备养一批供游客观赏的鱼，分别在AB、BC、CA上取点D，E，F，如图(1)，使得EF‖AB，EF⊥ED，在△DEF喂食，求△DEF 面积S△DEF的最大值；

    (2)现在准备新建造一个荷塘，分别在AB，BC，CA上取点D，E，F，如图(2)，建造△DEF

    连廊（不考虑宽度）供游客休憩，且使△DEF为正三角形，求△DEF边长的最小值．

    查看答案和解析>>

    同步练习册答案