
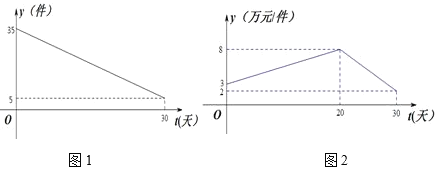
【题目】某商品近一个月内(30天)预计日销量![]() (件)与时间t(天)的关系如图1所示,单价
(件)与时间t(天)的关系如图1所示,单价![]() (万元/件)与时间t(天)的函数关系如图2所示,(t为整数)
(万元/件)与时间t(天)的函数关系如图2所示,(t为整数)
(1)试写出![]() 与
与![]() 的解析式;
的解析式;
(2)求此商品日销售额的最大值?
【答案】(1)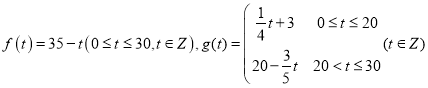 ;(2) 138万元.
;(2) 138万元.
【解析】
(1)根据直线上的点可求![]() 的解析式,根据分段函数以及一次函数可求
的解析式,根据分段函数以及一次函数可求![]() 的解析式;(2)根据
的解析式;(2)根据![]() ,可求求
,可求求![]() 的解析式,求出两段函数的值域,可得
的解析式,求出两段函数的值域,可得![]() 的最值.
的最值.
(1)由图象可知,
![]() ,
,
g(t)=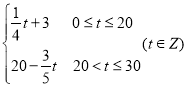
(2)设日销售额L(t)是天数t的函数,则有L(t)= f(t) ·g(t)=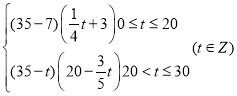
当0≤t≤20时,L(t)= 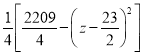 ,当t=11或12时,L(t)最大值为138万元,
,当t=11或12时,L(t)最大值为138万元,
当20<t≤30时,L(t)=![]() 在(20,30]是减函数,故L(t)<L(20)=120万元,故0≤t≤30时,当t=11或12时,L(t)最大值为138万元,
在(20,30]是减函数,故L(t)<L(20)=120万元,故0≤t≤30时,当t=11或12时,L(t)最大值为138万元,
答:第11天与第12天的日销售额最大,最大值为138万元.


科目:高中数学 来源: 题型:
【题目】盒子中仅有4个白球和5个黑球,从中任意取出一个球.
(1)“取出的球是黄球”是什么事件?它的概率是多少?
(2)“取出的球是白球”是什么事件?它的概率是多少?
(3)“取出的球是白球或黑球”是什么事件?它的概率是多少?
(4)设计一个用计算器或计算机模拟上面取球的试验,并模拟100次,估计“取出的球是白球”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为一个摩天轮示意图。该摩天轮圆半径为4.8m,圆上最低点与地面距离为0.8m,60s转动一周.图中OA与地面垂直。以O为始边,逆时针转动0角到OB设B点与地面的距离为hm.

(1)求h与![]() 的函数解析式;
的函数解析式;
(2)设从OA开始转动,经过ts到达OB,求h与t的函数解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,没售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损0.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了130吨该商品,现以![]() (单位:吨,
(单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
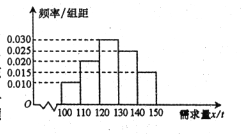
(Ⅰ)视![]() 分布在各区间内的频率为相应的概率,求
分布在各区间内的频率为相应的概率,求![]() ;
;
(Ⅱ)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(Ⅲ)在频率分布直方图的市场需求量分组中,以各组的区间中点值(组中值)代表该组的各个值,并以市场需求量落入该区间的频率作为市场需求量取该组中值的概率(例如![]() ,则取
,则取![]() 的概率等于市场需求量落入
的概率等于市场需求量落入![]() 的频率),求
的频率),求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com