Question

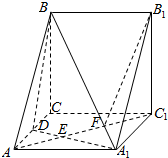
2．三棱柱ABC-A₁B₁C₁中，D是AC的中点，A₁D与AC₁交于点E，F在线段AC₁上，且AF=2FC₁．
（I）求证：B₁F∥平面A₁BD；
（Ⅱ）若AB=2，AC=1，∠ABC=30°，三棱锥B-A₁B₁E的体积为$\frac{\sqrt{3}}{2}$，求三棱柱ABC-A₁B₁C₁的高．

Answer 1

分析 （1）取A₁C₁中点G，连结CG，B₁C，B₁G，DG，则点F在CG上，证明平面B₁CG∥平面A₁BD，
（2）寻找三棱锥B-A₁B₁E的体积与三棱柱ABC-A₁B₁C₁的体积比例关系．

解答 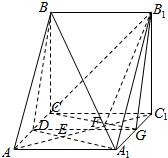证明：（1）取A₁C₁中点G，连结CG，B₁C，B₁G，DG，则点F在CG上，
∵D是AC的中点，G是A₁C₁的中点，
∴DG∥AA₁∥BB₁，DG=AA₁=BB₁，∴四边形DGB₁B是平行四边形，
∴B₁G∥BD，∵BD?平面A₁BD，B₁G?平面A₁BD，
∴B₁G∥平面A₁BD，
同理可证CG∥平面A₁BD，∵B₁G?平面B₁CG，CG?平面B₁CG，B₁G∩CG=G，
∴平面B₁CG∥平面A₁BD，∵B₁F?平面B₁CG，
∴B₁F∥平面A₁BD．
（2）∵$\frac{AC}{sin∠ABC}=\frac{AB}{sin∠ACB}$，∴$\frac{1}{\frac{1}{2}}=\frac{2}{sin∠ACB}$，解得sin∠ACB=1．∴AC⊥BC．
∴BC=AB•cos30°=$\frac{\sqrt{3}}{2}$，∴S_△ABC=$\frac{1}{2}$AC•BC=$\frac{\sqrt{3}}{2}$．
∵△ADE∽△C₁EA₁，∴$\frac{DE}{{A}_{1}E}$=$\frac{AD}{{A}_{1}{C}_{1}}$=$\frac{1}{2}$，∴$\frac{{A}_{1}E}{{A}_{1}D}$=$\frac{2}{3}$，
∴V${\;}_{棱锥D-AB{A}_{1}}$=V${\;}_{棱锥D-{A}_{1}B{B}_{1}}$=$\frac{3}{2}$V${\;}_{棱锥E-AB{B}_{1}}$=$\frac{3}{2}$V${\;}_{棱锥B-{A}_{1}{B}_{1}E}$=$\frac{3\sqrt{3}}{4}$．
设三棱柱ABC-A₁B₁C₁的高为h，
则V${\;}_{棱锥D-AB{A}_{1}}$=V${\;}_{棱锥{A}_{1}-ABD}$=$\frac{1}{3}$×$\frac{1}{2}$S_△ABC•h=$\frac{\sqrt{3}}{12}h$，
∴$\frac{\sqrt{3}}{12}h$=$\frac{3\sqrt{3}}{4}$，解得h=9．

点评 本题考查了线面平行的判定，体积计算，构造平面和寻找体积关系是关键．