
【题目】已知点![]() 在圆柱
在圆柱![]() 的底面圆
的底面圆![]() 上,
上,![]() 为圆
为圆![]() 的直径.
的直径.
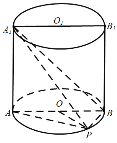
(1)求证:![]() ;
;
(2)若圆柱![]() 的体积
的体积![]() 为
为![]() ,
,![]() ,
,![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成的角(用反三角函数值表示结果).
所成的角(用反三角函数值表示结果).
【答案】(1)见解析;(2)![]()
【解析】
(1)根据圆柱的几何特征及圆周角定理,我们易根据已知中点P在圆柱![]() 的底面圆周上,AB为圆O的直径,得到AP⊥BP,
的底面圆周上,AB为圆O的直径,得到AP⊥BP,![]() ⊥BP,结合线面垂直的判定定理得到BP⊥平面
⊥BP,结合线面垂直的判定定理得到BP⊥平面![]() 后,易进一步得到BP⊥
后,易进一步得到BP⊥![]() ;
;
(2)延长PO交圆O于点Q,连接BQ,![]() ,结合圆柱的体积为
,结合圆柱的体积为![]()
![]() ,
,![]() ,我们易得∠
,我们易得∠![]() 即为异面直线
即为异面直线![]() 与
与![]() 所成角,利用余弦定理求出其余弦值,即可得到答案.
所成角,利用余弦定理求出其余弦值,即可得到答案.
解:解:(1)证明:易知AP⊥BP,
又由![]() ⊥平面PAB,
⊥平面PAB,
得![]() ⊥BP,
⊥BP,
从而BP⊥平面![]() ,
,
故BP⊥![]() ;
;
(2)解:延长PO交圆O于点Q,连接BQ,![]() ,
,
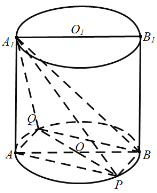
则BQ![]() AP,得∠
AP,得∠![]() 或它的补角为异面直线
或它的补角为异面直线![]() 与
与![]() 所成的角.
所成的角.
由题意![]() ,解得
,解得![]() =3.
=3.
又![]() ,则
,则![]() 为
为![]() 的直角三角形,
的直角三角形,
则![]() ,
,
得![]() ,
,
由余弦定理得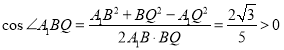 ,
,
则异面直线![]() 与
与![]() 所成的角为
所成的角为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
:![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,左、右两顶点分别是
,左、右两顶点分别是![]() 、
、![]() ,弦AB和CD所在直线分别平行于x轴与y轴,线段BA的延长线与线段CD相交于点
,弦AB和CD所在直线分别平行于x轴与y轴,线段BA的延长线与线段CD相交于点![]() 如图).
如图).
⑴若![]() 是
是![]() 的一条渐近线的一个方向向量,试求
的一条渐近线的一个方向向量,试求![]() 的两渐近线的夹角
的两渐近线的夹角![]() ;
;
⑵若![]() ,
,![]() ,
,![]() ,
,![]() ,试求双曲线
,试求双曲线![]() 的方程;
的方程;
⑶在⑴的条件下,且![]() ,点C与双曲线的顶点不重合,直线
,点C与双曲线的顶点不重合,直线![]() 和直线
和直线![]() 与直线l:
与直线l:![]() 分别相交于点M和N,试问:以线段MN为直径的圆是否恒经过定点?若是,请求出定点的坐标;若不是,试说明理由.
分别相交于点M和N,试问:以线段MN为直径的圆是否恒经过定点?若是,请求出定点的坐标;若不是,试说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两焦点分别为
的两焦点分别为![]() ,
,![]() ,
,![]() 是椭圆在第一象限内的一点,并满足
是椭圆在第一象限内的一点,并满足![]() ,过
,过![]() 作倾斜角互补的两直线
作倾斜角互补的两直线![]() 、
、![]() 分别交椭圆于
分别交椭圆于![]() 、
、![]() 两点.
两点.
(1)求![]() 点坐标;
点坐标;
(2)当直线![]() 经过点
经过点![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)求证直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.
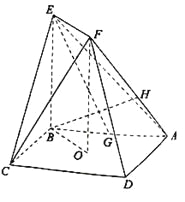
(Ⅰ)求证:EG∥平面ADF;
(Ⅱ)求二面角OEFC的正弦值;
(Ⅲ)设H为线段AF上的点,且AH=![]() HF,求直线BH和平面CEF所成角的正弦值.
HF,求直线BH和平面CEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】诚信是立身之本,道德之基,某校学生会创设了“诚信水站”,既便于学生用水,又推进诚信教育,并用“![]() ”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,下表为该水站连续十二周(共三个周期)的诚信数据统计:
”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,下表为该水站连续十二周(共三个周期)的诚信数据统计:
第一周 | 第二周 | 第三周 | 第四周 | |
第一个周期 |
|
|
|
|
第二个周期 |
|
|
|
|
第三个周期 |
|
|
|
|
(1)计算表中十二周“水站诚信度”的平均数![]() ;
;
(2)分别从表中每个周期的4个数据中随机抽取1个数据,设随机变量![]() 表示取出的3个数中“水站诚信度”超过
表示取出的3个数中“水站诚信度”超过![]() 的数据的个数,求随机变量
的数据的个数,求随机变量![]() 的分布列和期望;
的分布列和期望;
(3)已知学生会分别在第一个周期的第四周末和第二个周期的第四周末各举行了一次“以诚为本”的主题教育活动,根据已有数据,说明两次主题教育活动的宣传效果,并根据已有数据陈述理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部队在一次军演中要先后执行六项不同的任务,要求是:任务![]() 必须排在前三项执行,且执行任务
必须排在前三项执行,且执行任务![]() 之后需立即执行任务
之后需立即执行任务![]() ,任务
,任务![]() 、
、![]() 相邻,则不同的执行方案共有______种.
相邻,则不同的执行方案共有______种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业购买某种仪器,在仪器使用期间可能出现故障,需要请销售仪器的企业派工程师进行维修,因为考虑到人力、成本等多方面的原因,销售仪器的企业提供以下购买仪器维修服务的条件:在购买仪器时,可以直接购买仪器维修服务,维修一次1000元;在仪器使用期间,如果维修服务次数不够再次购买,则需要每次1500元..现需决策在购买仪器的同时购买几次仪器维修服务,为此搜集并整理了500台这种机器在使用期内需要维修的次数,得到如下表格:
维修次数 | 5 | 6 | 7 | 8 | 9 |
频数(台) | 50 | 100 | 150 | 100 | 100 |
记![]() 表示一台仪器使用期内维修的次数,
表示一台仪器使用期内维修的次数,![]() 表示一台仪器使用期内维修所需要的费用,
表示一台仪器使用期内维修所需要的费用,![]() 表示购买仪器的同时购买的维修服务的次数.
表示购买仪器的同时购买的维修服务的次数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)以这500台仪器使用期内维修次数的频率代替一台仪器维修次数发生的概率,求![]() 的概率.
的概率.
(3)假设购买这500台仪器的同时每台都购买7次维修服务,或每台都购买8次维修服务,请分别计算这500台仪器在购买维修服务所需要费用的平均数,以此为决策依据,判断购买7次还是8次维修服务?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,点F为抛物线的焦点,焦点F到直线3x-4y+3=0的距离为d1,焦点F到抛物线C的准线的距离为d2,且
,点F为抛物线的焦点,焦点F到直线3x-4y+3=0的距离为d1,焦点F到抛物线C的准线的距离为d2,且![]() 。
。
(1)抛物线C的标准方程;
(2)若在x轴上存在点M,过点M的直线l分别与抛物线C相交于P、Q两点,且![]() 为定值,求点M的坐标.
为定值,求点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,若动点
,若动点![]() 满足:
满足:![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 分别位于
分别位于![]() 轴与
轴与![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,请问在曲线
,请问在曲线![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() (
(![]() 为坐标原点)为平行四边形?若存在,求出直线
为坐标原点)为平行四边形?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com