
【题目】已知函数![]() ,
,![]() .
.
(1)求![]() 的最大值和最小值;
的最大值和最小值;
(2)若关于x的方程![]() 在
在![]() 上有两个不同的实根,求实数
上有两个不同的实根,求实数![]() 的取值范围.
的取值范围.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() ,
,![]() ,
,![]() ,
,![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.
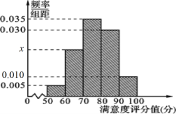
(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数的比为
内的男生数与女生数的比为![]() ,若在满意度评分值为
,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,在矩形
,在矩形![]() 中,
中, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起到
折起到![]() ,使得平面
,使得平面![]() 平面
平面![]() (如图
(如图![]() ).
).
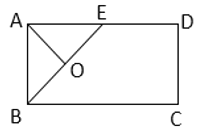
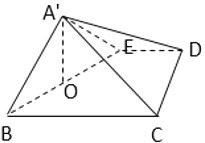
图1 图2
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: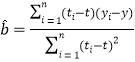 ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() 是集合
是集合![]()
![]() 的一个含有
的一个含有![]() 个元素的子集.
个元素的子集.
(Ⅰ)当![]() 时,
时,
设![]()
(i)写出方程![]() 的解
的解![]() ;
;
(ii)若方程![]() 至少有三组不同的解,写出
至少有三组不同的解,写出![]() 的所有可能取值.
的所有可能取值.
(Ⅱ)证明:对任意一个![]() ,存在正整数
,存在正整数![]() 使得方程
使得方程![]()
![]() 至少有三组不同的解.
至少有三组不同的解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项![]() ,
, ![]() ,
, ![]() .
.
(1)求证:数列 为等比数列;
为等比数列;
(2)记![]() ,若Sn<100,求最大正整数n;
,若Sn<100,求最大正整数n;
(3)是否存在互不相等的正整数m,s,n,使m,s,n成等差数列,且am-1,as-1,an-1成等比数列?如果存在,请给以证明;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(Ⅰ)求取出的两个球上标号为相同数字的概率;
(Ⅱ)求取出的两个球上标号之积能被3整除的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com