练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    与y轴相切并和圆x2+y2-10x=0外切的动圆圆心的轨迹是 （　　）
    A、圆B、抛物线
    C、双曲线D、抛物线和一条射线
    考点：轨迹方程
    专题：综合题,圆锥曲线的定义、性质与方程
    分析：分动圆在y轴右侧和动圆在y轴左侧两种情况考虑，若动圆在y轴右侧，则动圆圆心到定点（5，0）与到定直线x=-5的距离相等，利用抛物线的定义求轨迹方程，若动圆在y轴左侧，动圆圆心轨迹是x负半轴．
    解答： 解：若动圆在y轴右侧，则动圆圆心到定点（5，0）与到定直线x=-5的距离相等，其轨迹是抛物线，方程为y2=20x，
    若动圆在y轴左侧，则动圆圆心轨迹是x负半轴，方程为y=0，x≤0，
    故选：D．
    点评：本题考查轨迹方程的求法，以及抛物线定义的应用，体现分类讨论的数学思想．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    给出下列命题：
    ①若f′（x0）=0，则函数f（x）在x=x0处有极值；
    ②m＞0是方程
    x2
    m
    +
    y2
    4
    =1表示椭圆的充要条件；
    ③若f（x）=（x2-8）ex，则f（x）的单调递减区间为（-4，2）；
    ④双曲线
    x2
    a2
    -
    y2
    b2
    =1的离心率为e1，双曲线
    x2
    b2
    -
    y2
    a2
    =1的离心率为e2，则e1+e2的最小值为2
    		2

    其中为真命题的序号是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中如果∠B=
    π
    3
    ，b2=ac，则△ABC为
     
    三角形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若“x∈[1，5]或x∈{x|x＜-2或x＞3}”是假命题，则x的取值范围是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    关于“斜二测画法”，下列说法不正确的是（　　）
    A、原图形中平行于x轴的线段，其对应线段平行于x′轴，长度不变
    B、原图形中平行于y轴的线段，其对应线段平行于y′轴，长度变为原来的
    1
    2
    C、画与直角坐标系xOy对应的x′O′y′时，∠x′O′y′必须是45°
    D、在画直观图时，由于选轴的不同，所得的直观图可能不同

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    二项式（
    2
    x
    -x2）5展开式中的第四项的系数为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

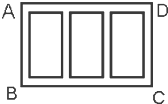    如图，某广场要划定一矩形区域ABCD，并在该区域内开辟出三块形状大小相同的小矩形绿化区，这三块绿化区四周和绿化区之间均设有1米宽的走道，已知三块绿化区的总面积为200平方米，求该矩形区域ABCD占地面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量
    a
    =（1，1），
    b
    =（0，-2），在下列条件下分别求k的值；
    （1）
    a
    +
    b
    与k
    a
    -
    b
    平行；
    （2）
    a
    +
    b
    与k
    a
    -
    b
    夹角为120°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在三角形ABC中，若a=
    		3
    ，cosA=
    1
    3
    ，则bc的最大值是
     
    ．

    查看答案和解析>>

    同步练习册答案