
【题目】已知函数![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)求函数![]() 在区间
在区间![]() 上的最大值
上的最大值![]() .
.
【答案】(1)见解析(2)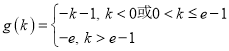
【解析】
(1)首先求出函数的导函数,令![]() 解得
解得![]() ,再对
,再对![]() 分类讨论即可得解;
分类讨论即可得解;
(2)对![]() 分类讨论,结合(1)中的结论,计算可得;
分类讨论,结合(1)中的结论,计算可得;
解:(1)因为![]() ,所以
,所以![]() ,
,
由![]() 解得
解得![]() .
.
①当![]() 时,
时,
|
|
|
|
| - | 0 | + |
|
| 极小值 |
|
所以,当![]() 时,
时,![]() 有极小值
有极小值![]() ;
;
②当![]() 时,
时,
|
|
|
|
| + | 0 | - |
|
| 极大值 |
|
所以,当![]() 时,
时,![]() 有极大值
有极大值![]() ;
;
综上,当![]() 时,当
时,当![]() 时,
时,![]() 有极小值
有极小值![]() ;
;
当![]() 时,当
时,当![]() 时,
时,![]() 有极大值
有极大值![]() .
.
(2)当![]() 时,由(1)知,
时,由(1)知,![]() 为
为![]() 上单调减函数,而
上单调减函数,而![]() ,
,
所以,![]() 为
为![]() 上单调减函数,故
上单调减函数,故![]() 的最大值
的最大值![]() ;
;
当![]() 时,
时,![]() ,由(1)知,
,由(1)知,![]() 为
为![]() 上单调减函数,而
上单调减函数,而![]() ,
,
所以,![]() 为
为![]() 上单调减函数,故
上单调减函数,故![]() 的最大值
的最大值![]() ;
;
当![]() 时,由(1)知,
时,由(1)知,![]() 为
为![]() 上单调减函数,
上单调减函数,![]() 上单调增函数,
上单调增函数,
又满足![]() ,故
,故![]() 的最大值
的最大值![]() ;
;
当![]() 时,由(1)知,
时,由(1)知,![]() 为
为![]() 上单调减函数,
上单调减函数,![]() 上单调增函数,
上单调增函数,
又满足![]() ,故
,故![]() 的最大值
的最大值![]() ;
;
综上,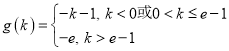 .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗,2020年春节前夕,A市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
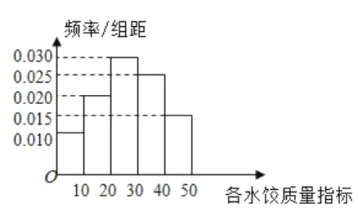
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|y=ln(﹣x2﹣x+12)},B={x|m﹣1<x<2m+1,m∈R}.
(1)若m=2,求(RA)∩B;
(2)若A∩B=B,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大西洋鲑鱼每年都要逆流而上,游回产地产卵,研究鲑鱼的科学家发现鲑鱼的游速![]() (单位:
(单位: ![]() )与其耗氧量单位数
)与其耗氧量单位数![]() 之间的关系可以表示为函数
之间的关系可以表示为函数![]() ,其中
,其中![]() 为常数,已知一条鲑鱼在静止时的耗氧量为100个单位;而当它的游速为
为常数,已知一条鲑鱼在静止时的耗氧量为100个单位;而当它的游速为![]() 时,其耗氧量为2700个单位.
时,其耗氧量为2700个单位.
(1)求出游速![]() 与其耗氧量单位数
与其耗氧量单位数![]() 之间的函数解析式;
之间的函数解析式;
(2)求当一条鲑鱼的游速不高于![]() 时,其耗氧量至多需要多少个单位?
时,其耗氧量至多需要多少个单位?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(多选)某中学高一年级有20个班,每班50人;高二年级有30个班,每班45人.甲就读于高一,乙就读于高二.学校计划从这两个年级中共抽取235人进行视力调查,下列说法中正确的有( )
A.应该采用分层随机抽样法
B.高一、高二年级应分别抽取100人和135人
C.乙被抽到的可能性比甲大
D.该问题中的总体是高一、高二年级的全体学生的视力
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,由四个全等的直角三角形和一个正方形构成.现有五种不同的颜色可供涂色,要求相邻的区域不能用同一种颜色,则不同的涂色方案有( )
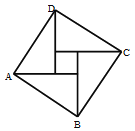
A.180B.192C.420D.480
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com