
【题目】在圆![]() 上任取一点
上任取一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线段,垂足为
轴的垂线段,垂足为![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() ,当点
,当点![]() 在圆上运动时.
在圆上运动时.
(1)求点![]() 的轨迹
的轨迹![]() 的方程,并指出轨迹
的方程,并指出轨迹![]() .
.
(2)直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.证明:直线OM的斜率与直线l的斜率的乘积为定值.
【答案】(1)![]() ,椭圆,(2)见解析.
,椭圆,(2)见解析.
【解析】
(1)设点![]() 的坐标为
的坐标为![]() ,由
,由![]() ,可得
,可得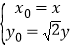 ,代入
,代入![]() 化简即可得结果;(2)设直线
化简即可得结果;(2)设直线![]() ,代入
,代入![]() 可得
可得![]() ,利用韦达定理以及中点坐标公式可得
,利用韦达定理以及中点坐标公式可得![]()
![]() ,从而可得结论.
,从而可得结论.
(1)设点![]() 的坐标为
的坐标为![]() ,
,
因为![]() 在圆上,所以
在圆上,所以![]()
设![]() ,因为
,因为![]() ,且
,且![]() 与
与![]() 轴垂直,
轴垂直,
所以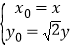 ,代入
,代入 ![]()
可得![]() ,化为
,化为![]() ,
,
即![]() 的方程为
的方程为![]() ,轨迹表示焦点在
,轨迹表示焦点在![]() 轴上的椭圆.
轴上的椭圆.
(2)设直线l:y=kx+b(k≠0,b≠0),A(x1,y1),B(x2,y2),M(xM,yM).
将y=kx+b代入![]() +
+![]() =1,得(2k2+1)x2+4kbx+2b2-8=0.
=1,得(2k2+1)x2+4kbx+2b2-8=0.
故xM=![]() =
=![]() ,yM=k·xM+b=
,yM=k·xM+b=![]() .
.
所以直线OM的斜率kOM=![]() =-
=-![]() ,
,
所以kOM·k=-![]() .
.
故直线OM的斜率与直线l的斜率的乘积为定值.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() 与直线
与直线![]() 的斜率分别记为
的斜率分别记为![]() 与
与![]() ,且
,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过定点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,
两点, ![]() 的面积是否存在最大值?若存在,求出
的面积是否存在最大值?若存在,求出![]() 面积的最大值;若不存在,请说明理由.
面积的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m, n是两条不同的直线,![]() 是三个不同的平面, 给出下列四个命题:
是三个不同的平面, 给出下列四个命题:
①若m⊥α,n∥α,则m⊥n;; ②若α∥β, β∥r, m⊥α,则m⊥r;
③若m∥α,n∥α,则m∥n;; ④若α⊥r, β⊥r,则α∥β.
其中正确命题的序号是 ( )
A. ![]() ①和② B. ②和③ C. ③和④ D. ①和④
①和② B. ②和③ C. ③和④ D. ①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .斜率为k的直线l与椭圆M有两个不同的交点A,B.
.斜率为k的直线l与椭圆M有两个不同的交点A,B.
(Ⅰ)求椭圆M的方程;
(Ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)设![]() ,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点
,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点![]() 共线,求k.
共线,求k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 的圆心,
的圆心, ![]() 是圆上的动点,点
是圆上的动点,点![]() 在圆的半径
在圆的半径![]() 上,且有点
上,且有点![]() 和
和![]() 上的点
上的点![]() ,满足
,满足![]() ,
, ![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)若斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 相切,直线
相切,直线![]() 与(1)中所求点
与(1)中所求点![]() 的轨迹交于不同的两点
的轨迹交于不同的两点![]() ,
, ![]() ,
, ![]() 是坐标原点,且
是坐标原点,且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“x∈R,ex>0”的否定是“x∈R,ex>0”
B.命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题
C.“x2+2x≥ax在x∈[1,2]上恒成立”“(x2+2x)min≥(ax)max在x∈[1,2]上恒成立”
D.命题“若a=﹣1,则函数f(x)=ax2+2x﹣1只有一个零点”的逆命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点到准线的距离为
的焦点到准线的距离为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线![]() 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点![]() .
.
(1)若![]() 的坐标为
的坐标为![]() ,求
,求![]() 的值;
的值;
(2)设线段![]() 的中点为
的中点为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,过
,过![]() 的直线
的直线![]() 与线段
与线段![]() 为直径的圆相切,切点为
为直径的圆相切,切点为![]() ,且直线
,且直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com