
【题目】第七届世界军人运动会(以下简称武汉军运会)专题新闻发布会在武汉举行,武汉军运会会徽、吉祥物正式公布.武汉军运会将于![]() 年
年![]() 月
月![]() 日举行,赛期
日举行,赛期![]() 天.若将
天.若将![]() 名志愿者分配到两个运动场馆进行服务,每个运动场馆至少
名志愿者分配到两个运动场馆进行服务,每个运动场馆至少![]() 名志愿者,则其中志愿者甲、乙或甲、丙被分到同一场馆的概率为______.
名志愿者,则其中志愿者甲、乙或甲、丙被分到同一场馆的概率为______.
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象上所有点的纵坐标不变,横坐标变为原来的
的图象上所有点的纵坐标不变,横坐标变为原来的![]() ,再将所得图象向右平移
,再将所得图象向右平移![]() 个单位,若得到的图象关于原点对称,则当
个单位,若得到的图象关于原点对称,则当![]() 时,
时,![]() 的值域为( )
的值域为( )
A.![]() B.
B.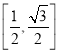 C.
C.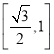 D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() ,
,![]() 的值;
的值;
(2)若函数![]() 在
在![]() 和
和![]() 两处取得极值,求实数
两处取得极值,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为直角梯形,
中,底面ABCD为直角梯形,![]()
![]() ,
,![]() 平面ABCD,E是棱PC上的一点.
平面ABCD,E是棱PC上的一点.
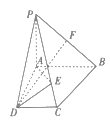
(1)证明:平面![]() 平面
平面![]() .
.
(2)若![]() ,F是PB的中点,
,F是PB的中点,![]() ,
,![]() ,求直线DF与平面
,求直线DF与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四面体![]() 中,
中, ![]() 分别是
分别是![]() 的中点.则下述结论:
的中点.则下述结论:
①四面体![]() 的体积为
的体积为![]() ;
;
②异面直线![]() 所成角的正弦值为
所成角的正弦值为![]() ;
;
③四面体![]() 外接球的表面积为
外接球的表面积为![]() ;
;
④若用一个与直线![]() 垂直,且与四面体的每个面都相交的平面
垂直,且与四面体的每个面都相交的平面![]() 去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为
去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为![]() .
.
其中正确的有_____.(填写所有正确结论的编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com