
【题目】已知函数![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .求实数
.求实数![]() 的值;
的值;
(2)①若![]() 时,函数
时,函数![]() 既有极大值,又有极小值,求实数
既有极大值,又有极小值,求实数![]() 的取值范围;
的取值范围;
②若![]() ,若
,若![]() 对一切正实数
对一切正实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围(用
的取值范围(用![]() 表示).
表示).
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏,将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
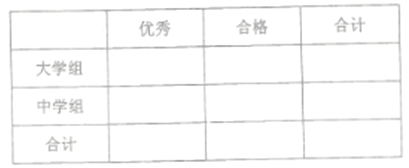
(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的![]() 列联表,并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
列联表,并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?


(2)若参赛选手共6万人,用频率估计概率,试估计其中优秀等级的选手人数;
(3)在优秀等级的选手中取6名,依次编号为1,2,3,4,5,6,在良好等级的选手中取6名,依次编号为1,2,3,4,5,6,在选出的6名优秀等级的选手中任取一名,记其编号为![]() ,在选出的6名良好等级的选手中任取一名,记其编号为
,在选出的6名良好等级的选手中任取一名,记其编号为![]() ,求使得方程组
,求使得方程组![]() 有唯一一组实数解
有唯一一组实数解![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在研究性学习中,关于三角形与三角函数知识的应用(约定三内角![]() 所对的边分别是
所对的边分别是![]() )得出如下一些结论:
)得出如下一些结论:
(1)若![]() 是钝角三角形,则
是钝角三角形,则![]() ;
;
(2)若![]() 是锐角三角形,则
是锐角三角形,则![]() ;
;
(3)在三角形![]() 中,若
中,若![]() ,则
,则![]()
(4)在![]() 中,若
中,若![]() ,则
,则![]()
其中错误命题的个数是 ( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,且
,且![]() .
.
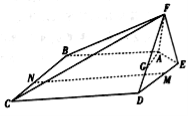
(1)已知点![]() 在线段
在线段![]() 上,确定
上,确定![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)点![]() 分别在线段
分别在线段![]() 上,若沿直线
上,若沿直线![]() 将四边形
将四边形![]() 向上翻折,
向上翻折,![]() 与
与![]() 恰好重合,求直线
恰好重合,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足![]() ,
,
(1)求数列{an}的通项公式;
(2)求证:数列{an}中的任意三项不可能成等差数列;
(3)设![]() ,Tn为{bn}的前n项和,求证
,Tn为{bn}的前n项和,求证![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,有下列结论:
,有下列结论:
①![]() 的最大值为
的最大值为![]() ;
;
②![]() 的最小正周期是
的最小正周期是![]() ;
;
③![]() 在区间
在区间![]() 上是减函数;
上是减函数;
④直线![]() 是函数
是函数![]() 的一条对称轴方程.
的一条对称轴方程.
其中正确结论的序号是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com