
【题目】抛物线y=x2﹣2xsinα+1的顶点在椭圆x2+my2=1上,这样的抛物线有且只有两条,则m的取值范围是_____.
【答案】(0,1)
【解析】
根据题意求出抛物线的顶点坐标,再代入椭圆的方程,即可得到cos2α=0或cos2α=![]() ,又因为对应的sinα有2个不同的值,所以看到cos2α=
,又因为对应的sinα有2个不同的值,所以看到cos2α=![]() 无解,进而得到答案.
无解,进而得到答案.
由题意可得:抛物线y=x2﹣2xsinα+1的顶点坐标为:(sinα,cos2α),
因为抛物线y=x2﹣2xsinα+1的顶点在椭圆x2+my2=1上,
所以将顶点代入椭圆方程可得:sin2α+mcos4α=1,即mcos4α=cos2α,
解得:cos2α=0或cos2α=![]() ,
,
因为这样的抛物线有且只有两条,
所以对应的sinα有2个不同的值,
所以cos2α=![]() 无解,即0<m<1.
无解,即0<m<1.
故答案为:(0,1).


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,无穷数列
,无穷数列![]() 的首项
的首项![]() .
.
(1)如果![]() ,写出数列
,写出数列![]() 的通项公式;
的通项公式;
(2)如果![]() (
(![]() 且
且![]() ),要使得数列
),要使得数列![]() 是等差数列,求首项
是等差数列,求首项![]() 的取值范围;
的取值范围;
(3)如果![]() (
(![]() 且
且![]() ),求出数列
),求出数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地计划在一处海滩建造一个养殖场.
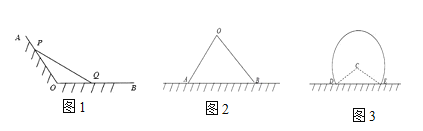
(1)如图1,射线OA,OB为海岸线,![]() ,现用长度为1千米的围网PQ依托海岸线围成一个
,现用长度为1千米的围网PQ依托海岸线围成一个![]() 的养殖场,问如何选取点P,Q,才能使养殖场
的养殖场,问如何选取点P,Q,才能使养殖场![]() 的面积最大,并求其最大面积.
的面积最大,并求其最大面积.
(2)如图2,直线l为海岸线,现用长度为1千米的围网依托海岸线围成一个养殖场.方案一:围成三角形OAB(点A,B在直线l上),使三角形OAB面积最大,设其为![]() ;方案二:围成弓形CDE(点D,E在直线l上,C是优弧所在圆的圆心且
;方案二:围成弓形CDE(点D,E在直线l上,C是优弧所在圆的圆心且![]() ),其面积为
),其面积为![]() ;试求出
;试求出![]() 的最大值和
的最大值和![]() (均精确到0.01平方千米),并指出哪一种设计方案更好.
(均精确到0.01平方千米),并指出哪一种设计方案更好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了鼓励职员工作热情,某公司对每位职员一年来的工作业绩按月进行考评打分;年终按照职员的月平均值评选公司最佳职员并给予相应奖励.已知职员![]() 一年来的工作业绩分数的茎叶图如图所示:
一年来的工作业绩分数的茎叶图如图所示:
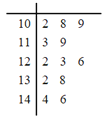
(1)根据职员![]() 的业绩茎叶图求出他这一年的工作业绩的中位数和平均数;
的业绩茎叶图求出他这一年的工作业绩的中位数和平均数;
(2)若记职员![]() 的工作业绩的月平均数为
的工作业绩的月平均数为![]() .
.
①已知该公司还有6位职员的业绩在100以上,分别是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,在这6人的业绩里随机抽取2个数据,求恰有1个数据满足
,在这6人的业绩里随机抽取2个数据,求恰有1个数据满足![]() (其中
(其中![]() )的概率;
)的概率;
②由于职员![]() 的业绩高,被公司评为年度最佳职员,在公司年会上通过抽奖形式领取奖金.公司准备了9张卡片,其中有1张卡片上标注奖金为6千元,4张卡片的奖金为4千元,另外4张的奖金为2千元.规则是:获奖职员需要从9张卡片中随机抽出3张,这3张卡片上的金额数之和就是该职员所得奖金.记职员
的业绩高,被公司评为年度最佳职员,在公司年会上通过抽奖形式领取奖金.公司准备了9张卡片,其中有1张卡片上标注奖金为6千元,4张卡片的奖金为4千元,另外4张的奖金为2千元.规则是:获奖职员需要从9张卡片中随机抽出3张,这3张卡片上的金额数之和就是该职员所得奖金.记职员![]() 获得的奖金为
获得的奖金为![]() (千元),求
(千元),求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】读书可以使人保持思想活力,让人得到智慧启发,让人滋养浩然正气书籍是文化的重要载体,读书是承继文化的重要方式某地区为了解学生课余时间的读书情况,随机抽取了![]() 名学生进行调查,根据调查得到的学生日均课余读书时间绘制成如图所示的频率分布直方图,将日均课余读书时间不低于
名学生进行调查,根据调查得到的学生日均课余读书时间绘制成如图所示的频率分布直方图,将日均课余读书时间不低于![]() 分钟的学生称为“读书之星”,日均课余读书时间低于
分钟的学生称为“读书之星”,日均课余读书时间低于![]() 分钟的学生称为“非读书之星”:已知抽取的样本中日均课余读书时间低于
分钟的学生称为“非读书之星”:已知抽取的样本中日均课余读书时间低于![]() 分钟的有
分钟的有![]() 人
人
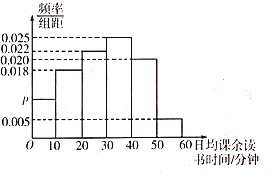
(1)求![]() 的值;
的值;
(2)根据已知条件完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“读书之星”与性别有关?
以上的把握认为“读书之星”与性别有关?
非读书之星 | 读书之星 | 总计 | |
男 | |||
女 |
|
| |
总计 |
(3)将上述调查所得到的频率视为概率,现从该地区大量学生中,随机抽取![]() 名学生,每次抽取
名学生,每次抽取![]() 名,已知每个人是否被抽到互不影响,记被抽取的“读书之星”人数为随机变量
名,已知每个人是否被抽到互不影响,记被抽取的“读书之星”人数为随机变量![]() ,求
,求![]() 的分布列和期望
的分布列和期望![]()
附: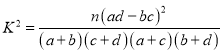 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
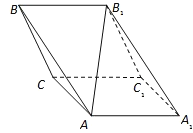
【题目】斜三棱柱ABC﹣A1B1C1,已知侧面BB1C1C与底面ABC垂直且∠BCA=90°,∠B1BC=60°,BC=BB1=2,若二面角A﹣B1B﹣C为30°
(1)求AB1与平面BB1C1C所成角的正切值;
(2)在平面AA1B1B内找一点P,使三棱锥P﹣BB1C为正三棱锥,并求P到平面BB1C距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当前,以“立德树人”为目标的课程改革正在有序推进.高中联招对初三毕业学生进行体育测试,是激发学生、家长和学校积极开展体育活动,保证学生健康成长的有效措施.某地区2019年初中毕业生升学体育考试规定,考生必须参加立定跳远、掷实心球、1分钟跳绳三项测试,三项考试满分为50分,其中立定跳远15分,掷实心球15分,1分钟跳绳20分.某学校在初三上期开始时要掌握全年级学生每分钟跳绳的情况,随机抽取了100名学生进行测试,得到如下频率分布直方图,且规定计分规则如下表:
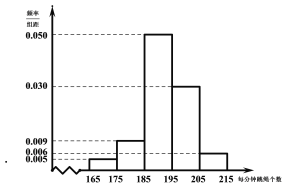
每分钟跳 绳个数 |
|
|
|
|
|
得分 | 16 | 17 | 18 | 19 | 20 |
(Ⅰ)现从样本的100名学生中,任意选取2人,求两人得分之和不大于33分的概率;
(Ⅱ)若该校初三年级所有学生的跳绳个数![]() 服从正态分布
服从正态分布![]() ,用样本数据的平均值和方差估计总体的期望和方差(结果四舍五入到整数),已知样本方差
,用样本数据的平均值和方差估计总体的期望和方差(结果四舍五入到整数),已知样本方差![]() (各组数据用中点值代替).根据往年经验,该校初三年级学生经过一年的训练,正式测试时每人每分钟跳绳个数都有明显进步,假设明年正式测试时每人每分钟跳绳个数比初三上学期开始时个数增加10个,利用现所得正态分布模型:
(各组数据用中点值代替).根据往年经验,该校初三年级学生经过一年的训练,正式测试时每人每分钟跳绳个数都有明显进步,假设明年正式测试时每人每分钟跳绳个数比初三上学期开始时个数增加10个,利用现所得正态分布模型:
(ⅰ)预估全年级恰好有1000名学生,正式测试时每分钟跳193个以上的人数.(结果四舍五入到整数)
(ⅱ)若在该地区2020年所有初三毕业生中任意选取3人,记正式测试时每分钟跳202个以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和期望.
的分布列和期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() ,则
,则![]() ,
,
![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选一个,补充在下面问题中的横线上,并解答相应的问题.
这三个条件中任选一个,补充在下面问题中的横线上,并解答相应的问题.
在![]() 中,内角A,B,C的对边分别为a,b,c,且满足________________,
中,内角A,B,C的对边分别为a,b,c,且满足________________,![]()
![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为椭圆
的焦点为椭圆![]() 的右焦点,且椭圆长轴的长为4,
的右焦点,且椭圆长轴的长为4,![]() 、
、![]() 是椭圆上的两点;
是椭圆上的两点;
(1)求椭圆标准方程;
(2)若直线![]() 经过点
经过点![]() ,且
,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)若动点![]() 满足:
满足:![]() ,直线
,直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,是否存在两个定点
,是否存在两个定点![]() 、
、![]() ,使得
,使得![]() 为定值?若存在,求出
为定值?若存在,求出![]() 、
、![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com