
分析 (1)化简函数的解析式,列出不等式组即可求解函数的定义域,函数的零点利用方程的根求解即可.
(2)利用零点定理以及构造函数通过二次函数的性质列出不等式组,即可求出结果.
解答 解:(1)、函数有意义,可得:$\left\{\begin{array}{l}x+1>0\\ 1-x>0\end{array}\right.$,所以函数的定义域D=(-1,1),
$F(x)=2{log_2}(x+1)-{log_2}(1-x)={log_2}\frac{{{{(x+1)}^2}}}{1-x}$,
$F(x)=0⇒\frac{{{{(1+x)}^2}}}{1-x}=1⇒{x^2}+3x=0⇒x=0$
函数的零点为0.
(2)、根据题意$m=\frac{{{{(1+x)}^2}}}{1-x},x∈[0,1)$,等价为x2+(m+2)x+1-m=0在[0,1)有解.
设h(x)=x2+(m+2)x+1-m,
①h(0)h(1)≤0⇒(1-m)(1+m+2+1-m)≤0⇒m≥1,
②$\left\{\begin{array}{l}△≥0\\ 0<-\frac{m+2}{2}<1\\ h(0)>0\\ h(1)>0\end{array}\right.⇒m∈ϕ$,∴m≥1.
点评 本题考查函数与方程的综合应用,函数的零点,以及根的分布,二次函数的性质的应用,考查计算能力.


 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
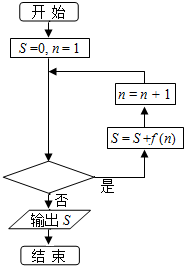 已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )
已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )| A. | n≤100? | B. | n≤99? | C. | n>100? | D. | n>99? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
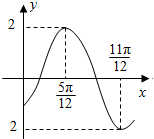 函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)的值是-$\sqrt{3}$.
函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)的值是-$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com