
【题目】已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是  (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值.
【答案】
(1)解:曲线C的极坐标方程是ρ=2cosθ,化为ρ2=2ρcosθ,可得直角坐标方程:x2+y2=2x.
直线L的参数方程是 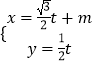 (t为参数),消去参数t可得
(t为参数),消去参数t可得 ![]()
(2)解:把 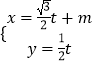 (t为参数),代入方程:x2+y2=2x化为:
(t为参数),代入方程:x2+y2=2x化为: ![]() +m2﹣2m=0,
+m2﹣2m=0,
由△>0,解得﹣1<m<3.
∴t1t2=m2﹣2m.
∵|PA||PB|=1=|t1t2|,
∴m2﹣2m=±1,
解得 ![]() ,1.又满足△>0.
,1.又满足△>0.
∴实数m=1 ![]() ,1
,1
【解析】(1)曲线C的极坐标方程是ρ=2cosθ,化为ρ2=2ρcosθ,利用 ![]() 可得直角坐标方程.直线L的参数方程是
可得直角坐标方程.直线L的参数方程是 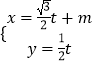 (t为参数),把t=2y代入
(t为参数),把t=2y代入 ![]() +m消去参数t即可得出.(2)把
+m消去参数t即可得出.(2)把 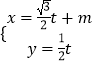 (t为参数),代入方程:x2+y2=2x化为:
(t为参数),代入方程:x2+y2=2x化为: ![]() +m2﹣2m=0,由△>0,得﹣1<m<3.利用|PA||PB|=t1t2 , 即可得出.
+m2﹣2m=0,由△>0,得﹣1<m<3.利用|PA||PB|=t1t2 , 即可得出.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的方程为(x﹣ ![]() )2+(y+1)2=9,以O为极点,x轴的非负半轴为极轴建立极坐标系.
)2+(y+1)2=9,以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线OP:θ= ![]() (p∈R)与圆C交于点M,N,求线段MN的长.
(p∈R)与圆C交于点M,N,求线段MN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的定义在实数集R上的奇函数,且当x∈(﹣∞,0)时,xf′(x)<f(﹣x)(其中f′(x)是f(x)的导函数),若a= ![]() f(
f( ![]() ),b=(lg3)f(lg3),c=(log2
),b=(lg3)f(lg3),c=(log2 ![]() )f(log2
)f(log2 ![]() ),则( )
),则( )
A.c>a>b
B.c>b>a
C.a>b>c
D.a>c>b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R.a,b∈R,若此函数同时满足:
①当a+b=0时,有f(a)+f(b)=0;
②当a+b>0时,有f(a)+f(b)>0,
则称函数f(x)为Ω函数.
在下列函数中:
①y=x+sinx;
②y=3x﹣( ![]() )x;
)x;
③y= 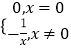
是Ω函数的为 . (填出所有符合要求的函数序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
求分数在[120,130)内的频率,并补全这个频
率分布直方图;
统计方法中,同一组数据常用该组区间的中点
值作为代表,据此估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段[120,130)内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣x,若对任意x1 , x2∈[2,+∞),且x1≠x2 , 不等式 ![]() >0恒成立,则实数a的取值范围是( )
>0恒成立,则实数a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于x的方程x2﹣ax﹣1=0和x2﹣x﹣2a=0的实根分别为x1、x2和x3、x4 , 若x1<x3<x2<x4 , 则实数a的取值范围为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com