
【题目】雅山中学采取分层抽样的方法从应届高三学生中按照性别抽出20名学生作为样本,其选报文科理科的情况如下表所示.
男 | 女 | |
文科 | 2 | 5 |
理科 | 10 | 3 |
(Ⅰ)若在该样本中从报考文科的学生中随机地选出3人召开座谈会,试求3人中既有男生也有女生的概率;
(Ⅱ)用假设检验的方法分析有多大的把握认为雅山中学的高三学生选报文理科与性别有关?
参考公式和数据:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.07 | 2.71 | 3.84 | 5.02 | 6.64 | 7.88 | 10.83 |
【答案】(Ⅰ)![]() ;(Ⅱ)有95%以上的把握认为学生选报文理科与性别有关.
;(Ⅱ)有95%以上的把握认为学生选报文理科与性别有关.
【解析】
试题(Ⅰ)设样本中两名男生分别为a,b,5名女生分别为c,d,e,f,g,则基本事件空间为;
(abc)(abd) (abe) (abf) (abg) (acd) (ace) (acf) (acg) (ade) (adf) (adg)
(aef) (aeg) (afg) (bcd) (bce) (bcf) (bcg) (bde) (bdf) (bdg) (bef) (beg)
(bfg) (cde) (cdf) (cdg) (cef) (ceg) (cfg) (def) (deg) (dfg) (efg)
共35种, 其中,既有男又有女的事件为前25种,
故P(“抽出的3人中既有男生也有女生”)=![]() =
=![]() .
.
(Ⅱ)![]()
![]() 4.43
4.43
![]() 3.841,
3.841,
对照参考表格,结合考虑样本是采取分层抽样抽出的,可知有95%以上的把握认为学生选报文理科与性别有关.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,AB=1,BC=2,AC![]() ,PC
,PC![]() ,PA
,PA![]() ,PB
,PB![]() ,E是线段BC的中点.
,E是线段BC的中点.
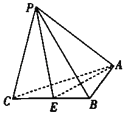
(1)求点C到平面APE的距离d;
(2)求二面角P﹣EA﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() (
(![]() ),
),![]() (
(![]() ),则下列说法中错误的是( )
),则下列说法中错误的是( )
A.若![]() ,则数列
,则数列![]() 为递增数列
为递增数列
B.若数列![]() 为递增数列,则
为递增数列,则![]()
C.存在实数![]() ,使数列
,使数列![]() 为常数数列
为常数数列
D.存在实数![]() ,使
,使![]() 恒成立
恒成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“黄梅时节家家雨”“梅雨如烟暝村树”“梅雨暂收斜照明”……江南梅雨的点点滴滴都流润着浓烈的诗情.每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南![]() 镇2009~2018年梅雨季节的降雨量(单位:
镇2009~2018年梅雨季节的降雨量(单位:![]() )的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
)的频率分布直方图,试用样本频率估计总体概率,解答下列问题:

![]() “梅实初黄暮雨深”.请用样本平均数估计
“梅实初黄暮雨深”.请用样本平均数估计![]() 镇明年梅雨季节的降雨量;
镇明年梅雨季节的降雨量;
![]() “江南梅雨无限愁”.
“江南梅雨无限愁”.![]() 镇的杨梅种植户老李也在犯愁,他过去种植的甲品种杨梅,他过去种植的甲品种杨梅,亩产量受降雨量的影响较大(把握超过八成).而乙品种杨梅2009~2018年的亩产量(
镇的杨梅种植户老李也在犯愁,他过去种植的甲品种杨梅,他过去种植的甲品种杨梅,亩产量受降雨量的影响较大(把握超过八成).而乙品种杨梅2009~2018年的亩产量(![]() /亩)与降雨量的发生频数(年)如
/亩)与降雨量的发生频数(年)如![]() 列联表所示(部分数据缺失).请你帮助老李排解忧愁,他来年应该种植哪个品种的杨梅受降雨量影响更小?
列联表所示(部分数据缺失).请你帮助老李排解忧愁,他来年应该种植哪个品种的杨梅受降雨量影响更小?
(完善列联表,并说明理由).
亩产量\降雨量 |
|
| 合计 |
<600 | 2 | ||
| 1 | ||
合计 | 10 |
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.703 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,若曲线
,若曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称.
对称.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,与
,与![]() 的异于极点的交点为
的异于极点的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位从一所学校招收某类特殊人才.对![]() 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
| 一般 | 良好 | 优秀 |
一般 |
|
|
|
良好 |
|
|
|
优秀 |
|
|
|
例如表中运动协调能力良好且逻辑思维能力一般的学生是![]() 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这![]() 位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)从运动协调能力为优秀的学生中任意抽取![]() 位,求其中至少有一位逻辑思维能力优秀的学生的概率.
位,求其中至少有一位逻辑思维能力优秀的学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年,国际权威机构IDC发布的全球手机销售报告显示:华为突破2亿台出货量超越苹果的出货量,首次成为全球第二,华为无愧于中国最强的高科技企业。华为业务CEO余承东明确表示,华为的目标,就是在2021年前,成为全球最大的手机厂商.为了解华为手机和苹果手机使用的情况是否和消费者的性别有关,对100名华为手机使用者和苹果手机使用者进行统计,统计结果如下表:
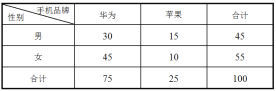
根据表格判断是否有95%的把握认为使用哪种品牌手机与性别有关系,则下列结论正确的是( )
附:![]()
![]()
A. 没有95%把握认为使用哪款手机与性别有关
B. 有95%把握认为使用哪款手机与性别有关
C. 有95%把握认为使用哪款手机与性别无关
D. 以上都不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com