
| x | 1 | 2 | 3 |
| y | 3 | 5.99 | 12.01 |
科目:高中数学 来源:不详 题型:解答题
 届亚运会于
届亚运会于 年
年 月
月 日至
日至 日在中国广州进行,为了做好接待工作,组委会招募了
日在中国广州进行,为了做好接待工作,组委会招募了 名男志愿者和
名男志愿者和 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有 人和
人和 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱. 列联表:
列联表:| | 喜爱运动 | 不喜爱运动 | 总计 |
| 男 | 10 | | 16 |
| 女 | 6 | | 14 |
| 总计 | | | 30 |
 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关? 人会外语),抽取
人会外语),抽取 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中 人都能胜任翻译工作的概率是多少?
人都能胜任翻译工作的概率是多少?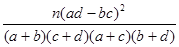
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
 ;
; )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
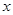 和年收入
和年收入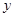 (万元),有以下的统计数据:
(万元),有以下的统计数据: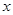 | 3 | 4 | 5 | 6 |
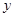 | 2.5 | 3 | 4 | 4.5 |
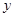 关于
关于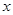 的线性回归方程
的线性回归方程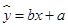 ;
;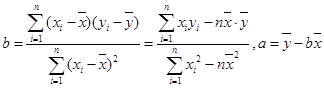 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.身高一定是145.83 cm | B.身高在145.83 cm以上 |
| C.身高在145.83 cm左右 | D.身高在145.83 cm以下 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,据此可以预测这个孩子10岁时的身高,则正确的叙述是( )
,据此可以预测这个孩子10岁时的身高,则正确的叙述是( ) | A.身高一定是145.83cm | B.身高超过146.00cm |
| C.身高低于145.00cm | D.身高在145.83cm左右 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 转速χ(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
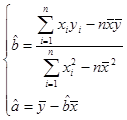
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
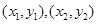 ,…,
,…,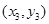 是变量
是变量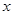 和
和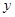 的
的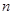 个样本点,直线
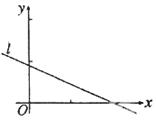
个样本点,直线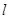 是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是 ( )
是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是 ( )A.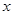 和 和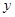 的相关系数为直线 的相关系数为直线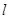 的斜率 的斜率 |
B.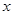 和 和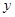 的相关系数在0到1之间 的相关系数在0到1之间 |
C.当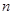 为偶数时,分布在 为偶数时,分布在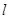 两侧的样本点的个数一定相同 两侧的样本点的个数一定相同 |
D.直线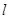 过点 过点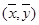 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com