练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，圆的方程为，若直线上至少存在一点，使得以该点为圆心，1为半径的圆与圆有公共点，则的最大值为__________．

    【答案】

    【解析】试题分析：由于圆C的方程为（x-4）2+y2=1，由题意可知，只需（x-4）2+y2=4与直线y=kx-2有公共点即可。解：∵圆C的方程为x2+y2-8x+15=0，整理得：（x-4）2+y2=1，即圆C是以（4，0）为圆心，1为半径的圆；又直线y=kx-2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，∴只需圆C′：（x-4）2+y2=4与直线y=kx-2有公共点即可．设圆心C（4，0）到直线y=kx-2的距离为d，

    即3k2≤4k，∴0≤k≤，故可知参数k的最大值为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知抛物线y=ax2+bx+c的图象如图所示，则|a﹣b+c|+|2a+b|=（　　）

    A.a+b
    B.a﹣2b
    C.a﹣b
    D.3a

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形ABCD是平行四边形，AE平分∠BAD，交DC的延长线于点E．求证：DA=DE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了更好地规划进货的数量，保证蔬菜的新鲜程度，某蔬菜商店从某一年的销售数据中，随机抽取了8组数据作为研究对象，如下图所示（（吨）为买进蔬菜的质量， （天）为销售天数）：

    2

    3

    4

    5

    6

    7

    9

    12

    1

    2

    3

    3

    4

    5

    6

    8

    （Ⅰ）根据上表数据在下列网格中绘制散点图；

    （Ⅱ）根据上表提供的数据，用最小二乘法求出关于的线性回归方程；

    （Ⅲ）根据（Ⅱ）中的计算结果，若该蔬菜商店准备一次性买进25吨，则预计需要销售多少天.

    参考公式： ， .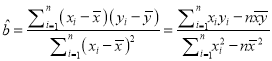

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg，乙材料1kg，用5个工时；生产一件产品B需要甲材料0.5kg，乙材料0.3kg，用3个工时.生产一件产品A的利润为2100元，生产一件产品B的利润为900元.该企业现有甲材料150kg，乙材料90kg，求在不超过600个工时的条件下，生产产品A和产品B的利润之和的最大值(元).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆： 的离心率与双曲线的离心率互为倒数，且椭圆的长轴长为4．

    （1）求椭圆的标准方程；

    （2）若直线交椭圆于， 两点， （）为椭圆上一点，求面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆方程为，双曲线的两条渐近线分别为， ，过椭圆的右焦点作直线，使，又与交于点，设直线与椭圆的两个交点由上至下依次为， ．　

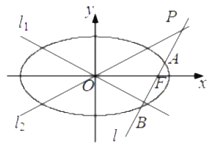
    （1）若与所成的锐角为，且双曲线的焦距为4，求椭圆的方程；

    （2）求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知sin（x﹣ ）= ，cos2x= ， （Ⅰ）求 的值；
    （Ⅱ）求 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： 经过点，左右焦点分别为、，圆与直线相交所得弦长为2．　

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）设是椭圆上不在轴上的一个动点， 为坐标原点，过点作的平行线交椭圆于、两个不同的点．

    （1）试探究的值是否为一个常数？若是，求出这个常数；若不是，请说明理由．

    （2）记的面积为， 的面积为，令，求的最大值．

    查看答案和解析>>

    同步练习册答案