
 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,离心率为$\frac{\sqrt{2}}{2}$,点A是椭圆C上任意一点,且△AF1F2的周长为2($\sqrt{2}$+1)
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,离心率为$\frac{\sqrt{2}}{2}$,点A是椭圆C上任意一点,且△AF1F2的周长为2($\sqrt{2}$+1)分析 (1)由题意可得:$e=\frac{\sqrt{2}}{2}$=$\frac{c}{a}$,a2=b2+c2,2a+2c=2$(\sqrt{2}+1)$,联立解出即可得出.
(2)设A(x0,y0),B$({x}_{1},\sqrt{2})$,由OA⊥OB,可得${x}_{0}{x}_{1}+\sqrt{2}{y}_{0}$=0,x1=-$\frac{\sqrt{2}{y}_{0}}{{x}_{0}}$.
分类讨论:①若x1≠x0,直线AB的方程为:y-$\sqrt{2}$=$\frac{{y}_{0}-\sqrt{2}}{{x}_{0}-{x}_{1}}$(x-x1),即$({y}_{0}-\sqrt{2})$x+(x1-x0)y+$\sqrt{2}{x}_{0}$-x1y0=0,利用点到直线的距离公式与${x}_{0}^{2}=2-2{y}_{0}^{2}$,可得d(A,B)为定值1.②若x1=x0,设直线OA的方程为:y=kx,则B$(\frac{\sqrt{2}}{k},\sqrt{2})$,A$(\frac{\sqrt{2}}{k},-\frac{\sqrt{2}}{{k}^{2}})$,代入椭圆方程解出k即可得出.
解答 (1)解:由题意可得:$e=\frac{\sqrt{2}}{2}$=$\frac{c}{a}$,a2=b2+c2,2a+2c=2$(\sqrt{2}+1)$,解得a=$\sqrt{2}$,c=b=1.
∴椭圆C的标准方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1.
(2)证明:设A(x0,y0),B$({x}_{1},\sqrt{2})$,
∵OA⊥OB,∴${x}_{0}{x}_{1}+\sqrt{2}{y}_{0}$=0.∴x1=-$\frac{\sqrt{2}{y}_{0}}{{x}_{0}}$.
①若x1≠x0,kAB=$\frac{{y}_{0}-\sqrt{2}}{{x}_{0}-{x}_{1}}$,直线AB的方程为:y-$\sqrt{2}$=$\frac{{y}_{0}-\sqrt{2}}{{x}_{0}-{x}_{1}}$(x-x1),
即$({y}_{0}-\sqrt{2})$x+(x1-x0)y+$\sqrt{2}{x}_{0}$-x1y0=0,
∴d(A,B)=$\frac{|\sqrt{2}{x}_{0}-{x}_{1}{y}_{0}|}{\sqrt{({y}_{0}-\sqrt{2})^{2}+({x}_{1}-{x}_{0})^{2}}}$,
∴[d(A,B)]2=$\frac{(\sqrt{2}{x}_{0}-{x}_{1}{y}_{0})^{2}}{({y}_{0}-\sqrt{2})^{2}+({x}_{1}-{x}_{0})^{2}}$=$\frac{2({x}_{0}^{2}+{y}_{0}^{2})^{2}}{{x}_{0}^{2}({y}_{0}-\sqrt{2})^{2}+(\sqrt{2}{y}_{0}+{x}_{0}^{2})}$,
∵${x}_{0}^{2}=2-2{y}_{0}^{2}$,
∴[d(A,B)]2=$\frac{2(2-{y}_{0}^{2})^{2}}{(2-2{y}_{0}^{2}){y}_{0}^{2}+4-2{y}_{0}^{2}+(2-2{y}_{0}^{2})^{2}}$=$\frac{2(2-{y}_{0}^{2})^{2}}{2(2-{y}_{0}^{2})^{2}}$=1,
∴d(A,B)=1,为定值.
②若x1=x0,设直线OA的方程为:y=kx,则B$(\frac{\sqrt{2}}{k},\sqrt{2})$,A$(\frac{\sqrt{2}}{k},-\frac{\sqrt{2}}{{k}^{2}})$,
代入椭圆方程可得:$\frac{2}{2{k}^{2}}$+$\frac{2}{{k}^{4}}$=1,解得k=$±\sqrt{2}$.
∴直线AB的方程为:x=±1,点O到直线AB的距离d(A,B)=1.
综上可得:d(A,B)为定值1.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、相互垂直的直线斜率之间的关系、点到直线的距离公式,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
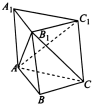 如图,已知三棱柱ABC-A1B1C1中,CA=CB,侧面AA1B1B是菱形,且∠ABB1=60°.
如图,已知三棱柱ABC-A1B1C1中,CA=CB,侧面AA1B1B是菱形,且∠ABB1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ρcosθ=$\frac{1}{2}$ | B. | ρcosθ=2 | C. | ρ=4sin(θ+$\frac{π}{3}$) | D. | ρ=4sin(θ-$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC,且AB⊥BC,O为AC中点,则直线A1C与平面A1AB所成角的正弦值为( )
如图,在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC,且AB⊥BC,O为AC中点,则直线A1C与平面A1AB所成角的正弦值为( )| A. | $\frac{3}{5}$ | B. | $\frac{\sqrt{21}}{7}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,$\frac{1}{4}$) | B. | (-1,$\frac{1}{2}$)∪(1,+∞) | C. | (-∞,-1)∪(4,+∞) | D. | (-1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (1,3) | C. | (-1,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,平行四边形ABCD中,AB=1,AD=4,CE=$\frac{1}{3}$CB.CF=$\frac{2}{3}$CD,∠DAB=60°,求$\overrightarrow{AC}$•$\overrightarrow{FE}$的值.
如图,平行四边形ABCD中,AB=1,AD=4,CE=$\frac{1}{3}$CB.CF=$\frac{2}{3}$CD,∠DAB=60°,求$\overrightarrow{AC}$•$\overrightarrow{FE}$的值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com