
(1)![]()
(2)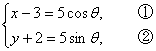
(3)
解:(1)由![]() 得
得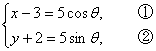
①2+②2,得(x-3)2+(y+2)2=25为所求普通方程.
(2)当a=0,b≠0时,x=0(y∈R);
当a≠0,b=0时,y=0(|x|≥|a|);
当a=0,b=0时,x=0且y=0;
当a≠0,b≠0时,由 得
得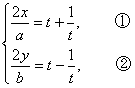
①2-②2,得![]() =1为所求普通方程.
=1为所求普通方程.
(3)由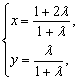 得
得
①-②,得x-y=1,即x-y-1=0.
由x=2-![]() ,x≠2.
,x≠2.
由y=1-![]() 知,y≠1.
知,y≠1.
故所求普通方程为x-y-1=0(x≠2).
点评:把参数方程化为普通方程,基本思路是消参数,常用的方法:利用三角恒等式如
sin2θ+cos2θ=1;利用代数恒等式如(t+![]() )2-(t-
)2-(t-![]() )2=4;或者利用代入消元、加减消元.如例1中(3),特别提醒:消元时注意x、y的范围.
)2=4;或者利用代入消元、加减消元.如例1中(3),特别提醒:消元时注意x、y的范围.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
 A:如图,已知AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.
A:如图,已知AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com