
【题目】在三棱锥![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,
,![]() ,则三棱锥ABCD体积的最大值是______.
,则三棱锥ABCD体积的最大值是______.
【答案】![]()
【解析】
过![]() 作与
作与![]() 垂直的平面,交
垂直的平面,交![]() 于
于![]() ,过
,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,则
,则![]() ,进而可分析出当
,进而可分析出当![]() 取最大值时,三棱锥
取最大值时,三棱锥![]() 的体积取最大值,又由
的体积取最大值,又由![]() ,可得B,C都在以A,D为焦点的椭圆上,利用椭圆的几何意义及勾股定理,求出的最大值即可得结果.
,可得B,C都在以A,D为焦点的椭圆上,利用椭圆的几何意义及勾股定理,求出的最大值即可得结果.
过BC作与AD垂直的平面,交AD于E,过E作BC的垂线,垂足为F,
如图所示:

![]() ,
,![]() ,则三棱锥
,则三棱锥![]() 的体积为
的体积为
![]() ,
,
故EF取最大值时,三棱锥![]() 的体积也取最大值.
的体积也取最大值.
由![]() ,
,
可得B,C都在以A,D为焦点的椭圆上,
因为平面BCE与线AD垂直,
所以三角形ADB与三角形ADC全等,即三角形BCE为等腰三角形,
又![]() 为定值,所以BE取最大值时,三棱锥
为定值,所以BE取最大值时,三棱锥![]() 的体积也取最大值.
的体积也取最大值.
在![]() 中,动点B到A,D两点的距离和为10,
中,动点B到A,D两点的距离和为10,
B在以AD为焦点的椭圆上(长轴、焦距分别为![]() 、
、![]() ),
),
此时![]() ,
,![]() ,
,
故BE的最大值为![]() ,
,
此时 ,
,
故三棱锥![]() 的体积的最大值是
的体积的最大值是![]() .
.
故答案为:![]()


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2x,过点E(a,0)的直线l与C交于不同的两点P(x1,y1),Q(x2,y2),且满足y1y2=﹣4,以Q为中点的线段的两端点分别为M,N,其中N在x轴上,M在C上,则a=_____.|PM|的最小值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场一年中各月份的收入、支出(单位:万元)情况的统计如折线图所示,则下列说法正确的是( )
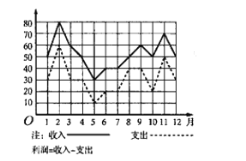
A.2至3月份的收入的变化率与11至12月份的收入的变化率相同
B.支出最高值与支出最低值的比是![]()
C.第三季度平均收入为60万元
D.利润最高的月份是2月份
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 若满足:①对任意
若满足:①对任意![]() 、
、![]() ,都有
,都有![]() ;②对任意
;②对任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 为“中心捺函数”,其中点
为“中心捺函数”,其中点![]() 称为函数
称为函数![]() 的中心.已知函数
的中心.已知函数![]() 是以
是以![]() 为中心的“中心捺函数”,若满足不等式
为中心的“中心捺函数”,若满足不等式![]() ,当
,当![]() 时,
时,![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知中心在原点,焦点在![]() 轴上的椭圆的一个焦点为
轴上的椭圆的一个焦点为![]() ,
, 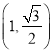 是椭圆上的一个点.
是椭圆上的一个点.
(1)求椭圆的标准方程;
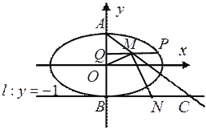
(2)设椭圆的上、下顶点分别为![]() ,
, ![]() (
(![]() )是椭圆上异于
)是椭圆上异于![]() 的任意一点,
的任意一点, ![]() 轴,
轴, ![]() 为垂足,
为垂足, ![]() 为线段
为线段![]() 中点,直线
中点,直线![]() 交直线
交直线![]() 于点
于点![]() ,
, ![]() 为线段
为线段![]() 的中点,如果
的中点,如果![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是![]() ,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,曲线C经过伸缩变换
,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,曲线C经过伸缩变换 得到曲线E,直线
得到曲线E,直线 (t为参数)与曲线E交于A,B两点.
(t为参数)与曲线E交于A,B两点.
(1)设曲线C上任一点为![]() ,求
,求![]() 的最小值;
的最小值;
(2)求出曲线E的直角坐标方程,并求出直线l被曲线E截得的弦AB长.
查看答案和解析>>
科目:高中数学 来源: 题型:
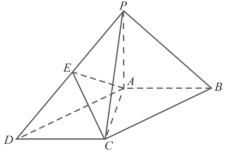
【题目】如图,在四棱锥![]() 中,
中,![]() 为平行四边形,
为平行四边形,![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上(不含端点)是否存在一点
上(不含端点)是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,确定
?若存在,确定![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种治疗新型冠状病毒感染肺炎的复方中药产品的质量以其质量指标值衡量,质量指标越大表明质量越好,为了提高产品质量,我国医疗科研专家攻坚克难,新研发出![]() 、
、![]() 两种新配方,在两种新配方生产的产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于
两种新配方,在两种新配方生产的产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于![]() 时为废品,指标值在
时为废品,指标值在![]() 为一等品,大于
为一等品,大于![]() 为特等品.现把测量数据整理如下,其中
为特等品.现把测量数据整理如下,其中![]() 配方废品有
配方废品有![]() 件.
件.
![]() 配方的频数分布表
配方的频数分布表
质量指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|

(1)求![]() ,
,![]() 的值;
的值;
(2)试确定![]() 配方和
配方和![]() 配方哪一种好?(说明:在统计方法中,同一组数据常用该组区间的中点值作为代表)
配方哪一种好?(说明:在统计方法中,同一组数据常用该组区间的中点值作为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 右顶点与上顶点,坐标原点
右顶点与上顶点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且点
,且点![]() 是圆
是圆![]() 的圆心,动直线
的圆心,动直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点.
两点.
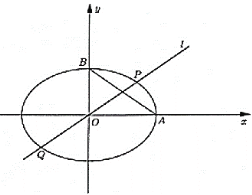
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 在线段
在线段![]() 上,
上,![]() ,且当
,且当![]() 取最小值时直线
取最小值时直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的值;
的值;
(3)若直线![]() 与圆
与圆![]() 分别交于
分别交于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 上,且
上,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com