
【题目】为了调查观众对某电视剧的喜爱程度,某电视台在甲乙两地随机抽取了8名观众做问卷调查,得分结果如图所示:
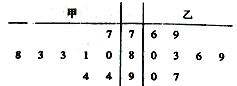
(1)计算甲地被抽取的观众问卷得分的中位数和乙地被抽取的观众问卷得分的平均数;
(2)若从乙地被抽取的8名观众中邀请2人参加调研,求参加调研的观众中恰有1人的问卷调查成绩在90分以上(含90分)的概率.
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,将曲线 ![]() (α为参数)上的每一点纵坐标不变,横坐标变为原来的一半,然后整个图象向右平移1个单位,最后横坐标不变,纵坐标变为原来的2倍得到曲线C1 . 以坐标原点为极点,x的非负半轴为极轴,建立的极坐标中的曲线C2的方程为ρ=4sinθ,求C1和C2公共弦的长度.
(α为参数)上的每一点纵坐标不变,横坐标变为原来的一半,然后整个图象向右平移1个单位,最后横坐标不变,纵坐标变为原来的2倍得到曲线C1 . 以坐标原点为极点,x的非负半轴为极轴,建立的极坐标中的曲线C2的方程为ρ=4sinθ,求C1和C2公共弦的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在冬季供暖时减少能量损耗,房屋的屋顶和外墙需要建造隔热层,某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:
(单位:![]() )满足关系:
)满足关系:![]() ,若不建隔热层,每年能源消耗费用为8万元,设
,若不建隔热层,每年能源消耗费用为8万元,设![]() 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 达到最小,并求最小值.
达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ![]() ,A(a,0),B(0,b),O(0,0),△OAB的面积为1.
,A(a,0),B(0,b),O(0,0),△OAB的面积为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P是椭圆C上一点,直线PA与y轴交于点M,直线PB与x轴交于点N.求证:|AN||BM|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等比数列,首项a1=1,公比q>0,其前n项和为Sn,且S1+a1,S3+a3,S2+a2成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足![]() ,Tn为数列{bn}的前n项和,若Tn≥m恒成立,求m的最大值.
,Tn为数列{bn}的前n项和,若Tn≥m恒成立,求m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个圆形波浪实验水池的中心有三个振动源,假如不计其它因素,在t秒内,它们引发的水面波动可分别由函数 ![]() 和
和 ![]() 描述,如果两个振动源同时启动,则水面波动由两个函数的和表达,在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现的状态是( )
描述,如果两个振动源同时启动,则水面波动由两个函数的和表达,在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现的状态是( )
A.仍保持平静
B.不断波动
C.周期性保持平静
D.周期性保持波动
查看答案和解析>>
科目:高中数学 来源: 题型:
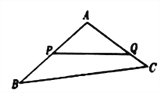
【题目】如图,某生态园将一块三角形地![]() 的一角
的一角![]() 开辟为水果园,已知角
开辟为水果园,已知角![]() 为
为![]() ,
, ![]() 的长度均大于200米,现在边界
的长度均大于200米,现在边界![]() 处建围墙,在
处建围墙,在![]() 处围竹篱笆.
处围竹篱笆.
(1)若围墙![]() 、
、![]() 总长度为200米,如何可使得三角形地块
总长度为200米,如何可使得三角形地块![]() 面积最大?
面积最大?
(2)已知竹篱笆长为![]() 米,
米, ![]() 段围墙高1米,
段围墙高1米, ![]() 段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com