
【题目】某市根据地理位置划分成了南北两区,为调查该市的一种经济作物![]() (下简称
(下简称![]() 作物)的生长状况,用简单随机抽样方法从该市调查了 500 处
作物)的生长状况,用简单随机抽样方法从该市调查了 500 处 ![]() 作物种植点,其生长状况如表:
作物种植点,其生长状况如表:

其中生长指数的含义是:2 代表“生长良好”,1 代表“生长基本良好”,0 代表“不良好,但仍有收成”,﹣1代表“不良好,绝收”.
(1)估计该市空气质量差的![]() 作物种植点中,不绝收的种植点所占的比例;
作物种植点中,不绝收的种植点所占的比例;
(2)能否有 99%的把握认为“该市![]() 作物的种植点是否绝收与所在地域有关”?
作物的种植点是否绝收与所在地域有关”?
(3)根据(2)的结论,能否提供更好的调查方法来估计该市![]() 作物的种植点中,绝收种植点的比例?请说明理由.
作物的种植点中,绝收种植点的比例?请说明理由.


【答案】(1) ![]() (2) 有99%的把握认为“该市A作物的种植点是否绝收与所在地域有关,(3) 采用分层抽样比采用简单随机抽样方法好.
(2) 有99%的把握认为“该市A作物的种植点是否绝收与所在地域有关,(3) 采用分层抽样比采用简单随机抽样方法好.
【解析】试题分析:(1)根据表格数据计算;
(2)采用独立检验方法列联表计算K2,与6.635比较大小得出结论;
(3)根据绝收比例可以看出采用分层抽样比较合理.
试题分析:
(1)调查的500处种植点中共有120处空气质量差,其中不绝收的共有110处,
∴空气质量差的A作物种植点中,不绝收的种植点所占的比例![]() .
.
(2)列联表如下:
收 | 绝收 | 合计 | |
南区 | 160 | 40 | 200 |
北区 | 270 | 30 | 300 |
合计 | 430 | 70 | 500 |
∴K2=![]() ≈9.967.
≈9.967.
∵9.967>6.635,
∴有99%的把握认为“该市A作物的种植点是否绝收与所在地域有关.
(3)由(2)的结论可知该市A作物的种植点是否绝收与所在地域有关,
因此在调查时,先确定该市南北种植比例,再把种植区分南北两层采用分层抽样比采用简单随机抽样方法好.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】在某次数学测验中,有6位同学的平均成绩为117分,用![]() 表示编号为
表示编号为![]() 的同学所得成 绩,6位同学成绩如表,
的同学所得成 绩,6位同学成绩如表,

(1)求![]() 及这6位同学成绩的方差;
及这6位同学成绩的方差;
(2)从这6位同学中随机选出2位同学,则恰有1位同学成绩在区间![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家举行大型的促销活动,经测算某产品当促销费用为![]() 万元时,销售量
万元时,销售量![]() 万件满足
万件满足![]() (其中
(其中![]() ,
, ![]() 为正常数),现假定生产量与销售量相等,已知生产该产品
为正常数),现假定生产量与销售量相等,已知生产该产品![]() 万件还需投入成本
万件还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 万元/万件.
万元/万件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
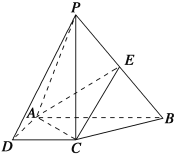
(1)求证:平面EAC⊥平面PBC;
(2)若二面角P-AC-E的余弦值为![]() ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数 ![]() ,看下面四个结论( ) ①f(x)是奇函数;②当x>2007时,
,看下面四个结论( ) ①f(x)是奇函数;②当x>2007时, ![]() 恒成立;③f(x)的最大值是
恒成立;③f(x)的最大值是 ![]() ;④f(x)的最小值是
;④f(x)的最小值是 ![]() .其中正确结论的个数为:
.其中正确结论的个数为:
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过A(3,2)、B(1,6),且圆心在直线y=2x上.
(1)求圆C的方程.
(2)若直线l经过点P(﹣1,3)与圆C相切,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C:x2+y2+4x﹣2y+m=0与直线x﹣ ![]() y+
y+ ![]() ﹣2=0相切.
﹣2=0相切.
(1)求圆C的方程;
(2)若圆C上有两点M,N关于直线x+2y=0对称,且|MN|=2 ![]() ,求直线MN的方程.
,求直线MN的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com