
【题目】随着甜品的不断创新,现在的甜品无论是造型还是口感都十分诱人,有颜值、有口味、有趣味的产品更容易得到甜品爱好者的喜欢,创新已经成为烘焙作品的衡量标准.某“网红”甜品店生产有几种甜品,由于口味独特,受到越来越多人的喜爱,好多外地的游客专门到该甜品店来品尝“打卡”,已知该甜品店同一种甜品售价相同,该店为了了解每个种类的甜品销售情况,专门收集了该店这个月里五种“网红甜品”的销售情况,统计后得如下表格:
甜品种类 | A甜品 | B甜品 | C甜品 | D甜品 | E甜品 |
销售总额(万元) | 10 | 5 | 20 | 20 | 12 |
销售额(千份) | 5 | 2 | 10 | 5 | 8 |
利润率 | 0.4 | 0.2 | 0.15 | 0.25 | 0.2 |
(利润率是指:一份甜品的销售价格减去成本得到的利润与该甜品的销售价格的比值.)
(1)从该甜品店本月卖出的甜品中随机选一份,求这份甜品的利润率高于0.2的概率;
(2)假设每类甜品利润率不变,销售一份A甜品获利![]() 元,销售一份B甜品获利
元,销售一份B甜品获利![]() 元,…,销售一份E甜品获利
元,…,销售一份E甜品获利![]() 元,设
元,设![]() ,若该甜品店从五种“网红甜品”中随机卖出2种不同的甜品,求至少有一种甜品获利超过
,若该甜品店从五种“网红甜品”中随机卖出2种不同的甜品,求至少有一种甜品获利超过![]() 的概率.
的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)计算本月总共卖出份数以及利率高于0.2的份数,然后简单计算,可得结果.
(2)计算每类甜品每份获利以及![]() ,然后利用列举法,列出“取出2种不同甜品”的所有可能结果,并计算“至少有一种甜品获利超过
,然后利用列举法,列出“取出2种不同甜品”的所有可能结果,并计算“至少有一种甜品获利超过![]() ”的个数,最后根据古典概型可得结果.
”的个数,最后根据古典概型可得结果.
(1)由题意知:本月共卖出3万份甜品,
利润率高于0.2的是A甜品和D甜品,共有1万份.
设“这份甜品利润率高于0.2”为事件A,
则![]() .
.
(2)由题意可得:每类甜品获利为8,5,3,10,3,
所以![]() ,
,
故A甜品与D甜品获利超过![]() ,
,
从五种“网红甜品”中随机卖出2种不同的甜品
共有以下10种不同的等可能结果:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
至少有一种甜品获利超过![]() 含有如下7种可能结果:
含有如下7种可能结果:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设“至少有一种甜品获利超过![]() ”为事件B,
”为事件B,
则![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,
中,![]() 底面ABC,
底面ABC,![]() ,E,F分别为棱PB,PC的中点,过E,F的平面分别与棱AB,AC相交于点D,G,给出以下四个结论:
,E,F分别为棱PB,PC的中点,过E,F的平面分别与棱AB,AC相交于点D,G,给出以下四个结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
则以上正确结论的个数是
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 且斜率为
且斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() :
:![]() 交椭圆
交椭圆![]() 于
于![]() 两点.
两点.

(1)求椭圆![]() 的方程;
的方程;
(2)求证:点![]() 在直线
在直线![]() 上;
上;
(3)是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在xOy中,曲线![]() 的参数方程为
的参数方程为![]() (t为参数).在以坐标原点O为极点,x轴正半轴为极轴的极坐标系中,曲线
(t为参数).在以坐标原点O为极点,x轴正半轴为极轴的极坐标系中,曲线![]() :
:![]() ,曲线
,曲线![]() :
:![]()
![]() ,
,![]() .
.
(1)把![]() 的参数方程化为极坐标方程;
的参数方程化为极坐标方程;
(2)设![]() 分别交
分别交![]() ,
,![]() 于点P,Q,求
于点P,Q,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(单位:分.百分制,均为整数)分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.
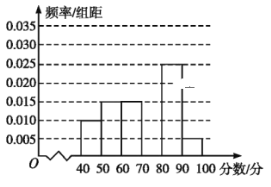
(1)求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的众数和平均数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的实轴端点分别为
的实轴端点分别为![]() ,记双曲线的其中一个焦点为
,记双曲线的其中一个焦点为![]() ,一个虚轴端点为
,一个虚轴端点为![]() ,若在线段
,若在线段![]() 上(不含端点)有且仅有两个不同的点
上(不含端点)有且仅有两个不同的点![]() ,使得
,使得![]() ,则双曲线的离心率
,则双曲线的离心率![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com