
(本小题满分12分)已知锐角△ABC中的三个内角分别为A,B,C.
(1)设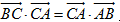 ,求证△ABC是等腰三角形;
,求证△ABC是等腰三角形;
(2)设向量s=(2sinC,-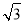 ),t=(cos2C,2
),t=(cos2C,2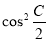 -1),且s∥t,若sinA=
-1),且s∥t,若sinA= ,求sin(
,求sin(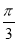 -B)的值.
-B)的值.
(1)见解析;(2)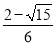
【解析】
试题分析:(1)根据条件,将向量的数量积转化为模长关系,证明两边长相等;(2)根据向量平行,对应坐标成比例,转化为三角函数关系式,结合三角形内角的关系,可求出sin(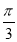 -B)的值
-B)的值
试题解析:(1)因为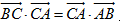 ,所以
,所以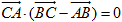
又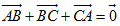 ,所以
,所以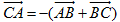
于是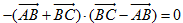
所以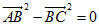 ,即
,即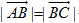
所以△ABC是等腰三角形.
(2)∵s∥t,∴2sinC(2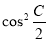 -1)=-
-1)=-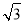 cos2C
cos2C
即2sinCcosC=-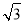 cos2C
cos2C
∴sin2C=-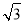 cos2C
cos2C
∴tan2C=-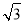
∵C是锐角,故2C∈(0,π),于是2C=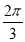
从而C=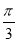 ,∴A=
,∴A=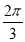 -B
-B
∴sin(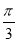 -B)=sin[(
-B)=sin[(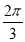 -B)-
-B)-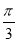 ]=sin(A-
]=sin(A-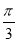 )
)
由sinA=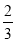 且A是锐角,故cosA=
且A是锐角,故cosA=
∴sin(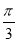 -B)=sin(A-
-B)=sin(A-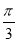 )=sinAcos
)=sinAcos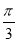 -cosAsin
-cosAsin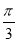 =
=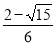
考点:三角函数恒等变形,和差角公式,二倍角公式,平面向量,解三角形


科目:高中数学 来源:2013-2014学年山东省烟台市高三统一质量检测考试理科数学试卷(解析版) 题型:选择题
已知圆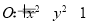 及以下三个函数:①
及以下三个函数:① ;②
;② ;③
;③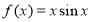 .其中图象能等分圆
.其中图象能等分圆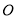 面积的函数个数为( )
面积的函数个数为( )
A.3 B.2 C.1 D.0
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考理科数学试卷(解析版) 题型:选择题
已知函数f(x)=sin(2x+Φ),其中Φ∈(0,2π),若f(x)≤|f(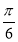 )|对一切x∈R恒成立,且f(
)|对一切x∈R恒成立,且f(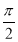 )<f(π),则f(x)的单调递增区间是( )
)<f(π),则f(x)的单调递增区间是( )
A、[kπ+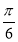 ,kπ+
,kπ+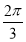 ](k∈Z)
](k∈Z)
B、[kπ-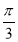 ,kπ+
,kπ+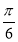 ](k∈Z)
](k∈Z)
C、[kπ,kπ+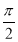 ](k∈Z)
](k∈Z)
D、[kπ-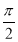 ,kπ](k∈Z)
,kπ](k∈Z)
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考理科数学试卷(解析版) 题型:选择题
集合A={x|x2+3x-10<0},B={x∈N|0<x+1<4},则A∩B=( )
A、{0,1,2} B、{-1,0,1} C、(-1,2) D、{0,1}
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考文科数学试卷(解析版) 题型:填空题
设f(x)= ,且f(8)=2,则f(f(80))=________________.
,且f(8)=2,则f(f(80))=________________.
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考文科数学试卷(解析版) 题型:选择题
下列命题中的假命题是( )
A、?x∈R,lgx=0
B、?x∈R,tanx=2
C、?x∈R,2x>0
D、?x∈R,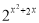 >1
>1
查看答案和解析>>
科目:高中数学 来源:2015届吉林省吉林市高三第一次摸底考试理科数学试卷(解析版) 题型:选择题
已知双曲线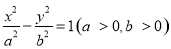 的左顶点与抛物线
的左顶点与抛物线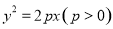 的焦点的距离为 4,的焦距是且双曲线的一条渐近线与抛物线的准线的交点坐标为 (-2,- 1),则双曲线的焦距为( )
的焦点的距离为 4,的焦距是且双曲线的一条渐近线与抛物线的准线的交点坐标为 (-2,- 1),则双曲线的焦距为( )
A. B.
B.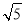 C.
C.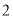 D.
D.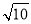
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com