
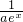 +b(a>0).
+b(a>0).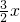 ,求a,b的值.
,求a,b的值.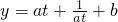
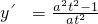
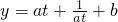 在t≥1上是增函数,
在t≥1上是增函数,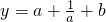
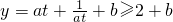 ,当且仅当at=1(x=-lna)时,f(x)的最小值为b+2;
,当且仅当at=1(x=-lna)时,f(x)的最小值为b+2;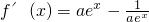
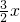 ,
,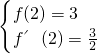 ,即
,即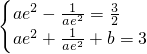 ,解得
,解得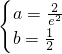 .
.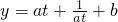 ,求出导函数
,求出导函数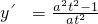 ,再进行分类讨论:①当a≥1时,y′>0,
,再进行分类讨论:①当a≥1时,y′>0,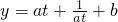 在t≥1上是增函数;②当0<a<1时,利用基本不等式
在t≥1上是增函数;②当0<a<1时,利用基本不等式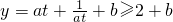 ,当且仅当at=1(x=-lna)时,f(x)取得最小值;
,当且仅当at=1(x=-lna)时,f(x)取得最小值;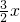 ,建立方程组,即可求得a,b的值.
,建立方程组,即可求得a,b的值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)| 5 |
| 3 |
| 5 |
| 3 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 12 |
| 7π |
| 12 |
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com