
 +
+ 代入f(x)•f(y)=f(x+y),可得(2)正确.再设x1,x2∈R,且x1<x2,则f(x1)-f(x2)=f[(x1-x2)+x2]-f(x2)=f(x2)[f(x1-x2)-1],
代入f(x)•f(y)=f(x+y),可得(2)正确.再设x1,x2∈R,且x1<x2,则f(x1)-f(x2)=f[(x1-x2)+x2]-f(x2)=f(x2)[f(x1-x2)-1], ,并且
,并且 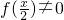 ,
,

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
| 1 | x+b |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.查看答案和解析>>
科目:高中数学 来源: 题型:
| x2+ax+1 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| x2-x-2 |
| lim |
| x→2 |
| 1 |
| x2-x-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com