
分析 利用几何概型,求出甲航班降落的时间窗口为上午10点到11点,如果它准点降落时间为上午10点40分,甲航班晚点的概率;试验包含的所有事件是Ω={(x,y)|0≤x≤1,0≤y≤1},做出事件对应的集合表示的面积,写出满足条件的事件是A={(x,y)|0≤x≤1,0≤y≤1,|x-y|≤$\frac{1}{4}$},算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.
解答  解:甲航班降落的时间窗口为上午10点到11点,如果它准点降落时间为上午10点40分,那么甲航班晚点的概率是$\frac{20}{60}$=$\frac{1}{3}$;
解:甲航班降落的时间窗口为上午10点到11点,如果它准点降落时间为上午10点40分,那么甲航班晚点的概率是$\frac{20}{60}$=$\frac{1}{3}$;
设甲乙两个航班到达的时间分别为(10+x)时、(10+y)时,
则0≤x≤1,0≤y≤1
若两架飞机降落时间间隔不超过15分钟,则|x-y|≤$\frac{1}{4}$
正方形的面积为1,落在两直线之间部分的面积为1-($\frac{3}{4}$)2=$\frac{7}{16}$,如图:
∴这两架飞机需要人工调度的概率是$\frac{7}{16}$.
故答案为$\frac{1}{3}$;$\frac{7}{16}$.
点评 本题是一个几何概型,对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{25}$ | B. | $\frac{4}{5}$ | C. | $\frac{9}{16}$ | D. | $\frac{9}{20}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
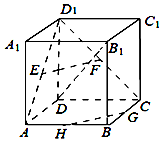 如图,已知正方体ABCD-A1B1C1D1,E,F,G,H分别是AD1、CD1、BC、AB的中点.
如图,已知正方体ABCD-A1B1C1D1,E,F,G,H分别是AD1、CD1、BC、AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
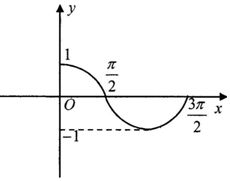 已知函数f(x)=sin(ωx+φ),x∈R(其中ω>0,-π<φ<π)的部分图象,如图所示.那么f(x)的解析式为( )
已知函数f(x)=sin(ωx+φ),x∈R(其中ω>0,-π<φ<π)的部分图象,如图所示.那么f(x)的解析式为( )| A. | $f(x)=sin(x+\frac{π}{2})$ | B. | $f(x)=sin(x-\frac{π}{2})$ | C. | $f(x)=sin(2x+\frac{π}{2})$ | D. | $f(x)=sin(2x-\frac{π}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com