
【题目】某学生对一些对数进行运算,如图表格所示:
x | 0.21 | 0.27 | 1.5 | 2.8 |
lgx | 2a+b+c﹣3(1) | 6a﹣3b﹣2(2) | 3a﹣b+c(3) | 1﹣2a+2b﹣c(4) |
x | 3 | 5 | 6 | 7 |
lgx | 2a﹣b(5) | a+c(6) | 1+a﹣b﹣c(7) | 2(a+c)(8) |
x | 8 | 9 | 14 | |
lgx | 3﹣3a﹣3c(9) | 4a﹣2b(10) | 1﹣a+2b(11) |
现在发觉学生计算中恰好有两次地方出错,那么出错的数据是( )
A.(3),(8)
B.(4),(11)
C.(1),(3)
D.(1),(4)
【答案】A
【解析】解:由题意可知:lg0.21=lg3+lg7﹣1=2a+b+c﹣3;
lg0.27=3lg3﹣2=6a﹣3b﹣2;
lg1.5=lg3+lg5﹣1=3a﹣b+c
lg2.8=2lg2+lg7﹣1,
lg3=2a﹣b,
lg5=a+c
lg6=lg2+lg3=1+a﹣b﹣c,
lg7=2a+2c,
lg8=3﹣3a﹣3c,
lg9=2lg3=4a﹣2b,
lg14=lg2+lg7=1﹣a+2b.
有上述各式,可以看出,lg3,lg9,lg0.27是正确的关系式,则lg7=2a+2c,lg0.21=lg3+lg7﹣1=2a+b+c﹣3,可知lg7错误;
由lg5=a+c,lg1.5=lg3+lg5﹣1=3a﹣b+c,可知lg5错误;
即(3),(8)错误.
故选:A.
【考点精析】关于本题考查的对数的运算性质,需要了解①加法:![]() ②减法:
②减法:![]() ③数乘:
③数乘:![]() ④
④![]() ⑤
⑤![]() 才能得出正确答案.
才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,已知 ![]() a=2csinA.
a=2csinA.
(1)求角C的值;
(2)若c= ![]() ,且S△ABC=
,且S△ABC= ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线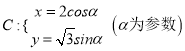 和定点
和定点![]() ,
, ![]() 是此曲线的左、右焦点,以原点
是此曲线的左、右焦点,以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求直线![]() 的极坐标方程;
的极坐标方程;
(2)经过点![]() 且与直线
且与直线![]() 垂直的直线交此圆锥曲线于
垂直的直线交此圆锥曲线于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)+f(x)≤0,对任意正数a、b,若a<b,则必有( )
A.af(b)≤bf(a)
B.bf(a)≤af(b)
C.af(a)≤f(b)
D.bf(b)≤f(a)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:如图,两同心圆: ![]() 和
和![]() .
. ![]() 为大圆上一动点,连结
为大圆上一动点,连结![]() (
(![]() 为坐标原点)交小圆于点
为坐标原点)交小圆于点![]() ,过点
,过点![]() 作
作![]() 轴垂线
轴垂线![]() (垂足为
(垂足为![]() ),再过点
),再过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() .
.

(1)当点![]() 在大圆上运动时,求垂足
在大圆上运动时,求垂足![]() 的轨迹方程;
的轨迹方程;
(2)过点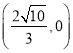 的直线
的直线![]() 交垂足
交垂足![]() 的轨迹于
的轨迹于![]() 两点,若以
两点,若以![]() 为直径的圆与
为直径的圆与![]() 轴相切,求直线
轴相切,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com