
【题目】将函数![]() 图象上的所有点的横坐标伸长到原来的2倍,再把所得各点向右平移
图象上的所有点的横坐标伸长到原来的2倍,再把所得各点向右平移![]() 个单位长度,最后把所得各点纵坐标扩大到原来的2倍,就得到函数f(x)的图象,则下列说法中正确的个数是( )
个单位长度,最后把所得各点纵坐标扩大到原来的2倍,就得到函数f(x)的图象,则下列说法中正确的个数是( )
①函数f(x)的最小正周期为2π;
②函数f(x)的最大值为2;
③函数f(x)图象的对称轴方程为![]() ;
;
④设x1,x2为方程![]() 的两个不相等的根,则
的两个不相等的根,则![]() 的最小值为
的最小值为![]() .
.
A.1B.2C.3D.4
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如右图所示.经销商为下一个销售季度购进了130t该农产品.以x(单位:t,100≤x≤150)表示下一个销售季度内经销该农产品的数量,T表示利润.
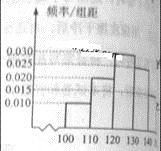
(Ⅰ)将T表示为x的函数
(Ⅱ)根据直方图估计利润T不少于57000元的概率;
(Ⅲ)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x![]() ,则取x=105,且x=105的概率等于需求量落入[100,110
,则取x=105,且x=105的概率等于需求量落入[100,110![]() ,求T的数学期望.
,求T的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近些年学区房的出现折射出现行教育体制方面的弊端造成了教育资源的分配不均衡.为此某市出台了政策:自2019年1月1日起,在该市新登记并取得房屋不动产权证书的住房用于申请入学的将不再对应一所学校,实施多校划片.有关部门调查了该市某名校对应学区内建筑面积不同的户型,得到了以下数据:
![]()
(1)试建立房屋价格y关于房屋建筑面积的x的线性回归方程;
(2)若某人计划消费不超过100万元购置学区房,根据你得到的回归方程估计此人选房时建筑面积最大为多少?(保留到小数点后一位数字)
参考公式: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,人们支付方式发生巨大转变,使用移动支付购买商品已成为一部分人的消费习惯,某企业为了解该企业员工![]() 两种移动支付方式的使用情况,从全体员工中随机抽取了100人,统计了他们在某个月的消费支出情况,发现样本中
两种移动支付方式的使用情况,从全体员工中随机抽取了100人,统计了他们在某个月的消费支出情况,发现样本中![]() 两种支付方式都没有使用过的有5人;使用了
两种支付方式都没有使用过的有5人;使用了![]() 两种方式支付的员工,支付金额和相应人数分布如下表,依据数据估算:若从该公司随机抽取1名员工,则该员工在该月
两种方式支付的员工,支付金额和相应人数分布如下表,依据数据估算:若从该公司随机抽取1名员工,则该员工在该月![]() 两种支付方式都使用过的概率为_______________
两种支付方式都使用过的概率为_______________
支付金额(元) 支付方式 |
|
| 大于2000 |
使用 | 18人 | 29人 | 23人 |
使用 | 10人 | 24人 | 21人 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校实行选科走班制度,张毅同学的选择是物理生物政治这三科,且物理在 A 层班级,生物在 B 层班级,该校周一上午课程安排如下表所示,张毅选择三个科目的课各上一节, 另外一节上自习,则他不同的选课方法有( )
第一节 | 第二节 | 第三节 | 第四节 |
地理 B 层 2 班 | 化学 A 层 3 班 | 地理 A 层 1 班 | 化学 A 层 4 班 |
生物 A 层 1 班 | 化学 B 层 2 班 | 生物 B 层 2 班 | 历史 B 层 1 班 |
物理 A 层 1 班 | 生物 A 层 3 班 | 物理 A 层 2 班 | 生物 A 层 4 班 |
物理 B 层 2 班 | 生物 B 层 1 班 | 物理 B 层 1 班 | 物理 A 层 4 班 |
政治 1 班 | 物理 A 层 3 班 | 政治 2 班 | 政治 3 班 |
A.8 种B.10 种C.12 种D.14 种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴为
的长轴为![]() ,
,![]() 分别为椭圆C的左、右顶点,P是椭圆C上异于
分别为椭圆C的左、右顶点,P是椭圆C上异于![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆C的方程;
(2)过点![]() 的直线l交椭圆C于
的直线l交椭圆C于![]() 两点,D为椭圆上一点,O为坐标原点,且满足
两点,D为椭圆上一点,O为坐标原点,且满足![]() ,其中
,其中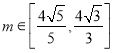 ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+bx(a>0,b>0,a≠1,b≠1).设a=2,b=![]() .
.
(1)求方程f(x)=2的根;
(2)若对于任意x∈R,不等式f(2x)≥mf(x)-6恒成立,求实数m的最大值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com