
| 4-π |
| 4 |
| 4-π |
| 4 |


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
| x |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省部分重点中学高二(上)期中数学试卷(文科)(解析版) 题型:选择题
 ,现用随机模拟的方法估计y=f(x)与x=4及x轴围成的面积S,用计算机先产生两组(每组30个)在区间[0,4]上的均匀随机数x1,x2,…,x30和y1,y2,…,y30,由此得到30个点(xi,yi)(i=1,2,…,30),现数出其中满足yi≤f(xi)(i=1,2,…,30)的点有10个,则由随机模拟的方法可估计得到面积S为( )
,现用随机模拟的方法估计y=f(x)与x=4及x轴围成的面积S,用计算机先产生两组(每组30个)在区间[0,4]上的均匀随机数x1,x2,…,x30和y1,y2,…,y30,由此得到30个点(xi,yi)(i=1,2,…,30),现数出其中满足yi≤f(xi)(i=1,2,…,30)的点有10个,则由随机模拟的方法可估计得到面积S为( )

查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省部分重点中学高二(上)期中数学试卷(理科)(解析版) 题型:选择题
 ,现用随机模拟的方法估计y=f(x)与x=4及x轴围成的面积S,用计算机先产生两组(每组30个)在区间[0,4]上的均匀随机数x1,x2,…,x30和y1,y2,…,y30,由此得到30个点(xi,yi)(i=1,2,…,30),现数出其中满足yi≤f(xi)(i=1,2,…,30)的点有10个,则由随机模拟的方法可估计得到面积S为( )
,现用随机模拟的方法估计y=f(x)与x=4及x轴围成的面积S,用计算机先产生两组(每组30个)在区间[0,4]上的均匀随机数x1,x2,…,x30和y1,y2,…,y30,由此得到30个点(xi,yi)(i=1,2,…,30),现数出其中满足yi≤f(xi)(i=1,2,…,30)的点有10个,则由随机模拟的方法可估计得到面积S为( )

查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省部分重点中学高二(上)期中数学试卷(文科)(解析版) 题型:选择题
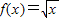 ,现用随机模拟的方法估计y=f(x)与x=4及x轴围成的面积S,用计算机先产生两组(每组30个)在区间[0,4]上的均匀随机数x1,x2,…,x30和y1,y2,…,y30,由此得到30个点(xi,yi)(i=1,2,…,30),现数出其中满足yi≤f(xi)(i=1,2,…,30)的点有10个,则由随机模拟的方法可估计得到面积S为( )
,现用随机模拟的方法估计y=f(x)与x=4及x轴围成的面积S,用计算机先产生两组(每组30个)在区间[0,4]上的均匀随机数x1,x2,…,x30和y1,y2,…,y30,由此得到30个点(xi,yi)(i=1,2,…,30),现数出其中满足yi≤f(xi)(i=1,2,…,30)的点有10个,则由随机模拟的方法可估计得到面积S为( )

查看答案和解析>>
科目:高中数学 来源: 题型:
学生晓东爱打篮球,假设其每次投篮命中的概率是40%,我们用1,2,3,4表示投中,用5,6,7,8,9,0表示未投中,用计算机随机产生以下20组随机数,可以估计晓东在连续三次投篮中,恰有两次投中的概率是多少? ( )
812,932,569,683,271,989,730,537,925,264
907,113,966,191,431,257,393,278,027,556.
A. 20% B.25% C.30% D.40%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com