
【题目】下列函数值域是(0,+∞)的是( )
A.y= ![]()
B.y=( ![]() )1﹣2x
)1﹣2x
C.y= ![]()
D.y= ![]()
科目:高中数学 来源: 题型:
【题目】设f(x)= ![]() (a>0,b>0).
(a>0,b>0).
(1)当a=b=1时,证明:f(x)不是奇函数;
(2)设f(x)是奇函数,求a与b的值;
(3)在(2)的条件下,试证明函数f(x)的单调性,并解不等式f(1﹣m)+f(1+m2)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]()
![]() 过点
过点![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,离心率
,离心率![]() ,
, ![]() 是椭圆右准线上的两个动点,且
是椭圆右准线上的两个动点,且![]() .
.
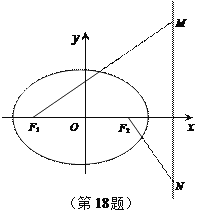
(1)求椭圆的方程;
(2)求![]() 的最小值;
的最小值;
(3)以![]() 为直径的圆
为直径的圆![]() 是否过定点?请证明你的结论.
是否过定点?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校对甲、乙两个班级进行了物理测验,成绩统计如下(每班50人):
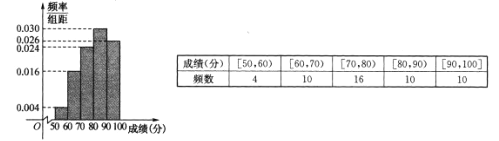
(1)估计甲班的平均成绩;
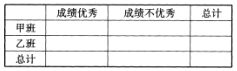
(2)成绩不低于80分记为“优秀”.请完成下面的![]() 列联表,并判断是否有85%的把握认为:“成绩优秀”与所在教学班级有关?
列联表,并判断是否有85%的把握认为:“成绩优秀”与所在教学班级有关?
(3)从两个班级,成绩在![]() 的学生中任选2人,记事件
的学生中任选2人,记事件![]() 为“选出的2人中恰有1人来自甲班”.求事件
为“选出的2人中恰有1人来自甲班”.求事件![]() 的概率
的概率![]() .
.
附: 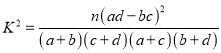
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产甲、乙两种桶装产品,已知生产甲产品1桶需耗![]() 原料2千克,
原料2千克, ![]() 原料3千克;生产乙产品1桶需耗
原料3千克;生产乙产品1桶需耗![]() 原料2千克,
原料2千克, ![]() 原料1千克,每桶甲产品的利润是300元,每桶乙产品的利润是400元,公司在要求每天消耗
原料1千克,每桶甲产品的利润是300元,每桶乙产品的利润是400元,公司在要求每天消耗![]() 原料都不超过12千克的条件下,生产产品
原料都不超过12千克的条件下,生产产品![]() 、产品
、产品![]() 的利润之和的最大值为( )
的利润之和的最大值为( )
A. 1800元 B. 2100元 C. 2400元 D. 2700元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=loga(1﹣x)+loga(x+3),(0<a<1).
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣2,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com