
【题目】下列四组函数中,表示同一函数的是( )
A.f(x)=x0与g(x)=1
B.f(x)=x与g(x)= ![]()
C.f(x)=x2﹣1与g(x)=x2+1
D.f(x)=|x|与g(x)= ![]()
【答案】D
【解析】解:对于A:f(x)=x0的定义域为{x|x≠0},而g(x)=1定义域为R,它们的定义域不同,∴不是同一函数; 对于B:f(x)=x的定义域为R,而g(x)= ![]() 定义域为{x|x≠0},它们的定义域不同,∴不是同一函数;
定义域为{x|x≠0},它们的定义域不同,∴不是同一函数;
对于C:f(x)=x2﹣1和g(x)=x2+1的定义域都是R,它们的定义域相同,但对应关系不同,∴不是同一函数;
对于D:f(x)=|x|和g(x)= ![]() 的定义域都是R,它们的定义域相同,对应关系也相同,∴是同一函数;
的定义域都是R,它们的定义域相同,对应关系也相同,∴是同一函数;
故选D.
【考点精析】利用判断两个函数是否为同一函数对题目进行判断即可得到答案,需要熟知只有定义域和对应法则二者完全相同的函数才是同一函数.


科目:高中数学 来源: 题型:
【题目】如图,已知复平面内平行四边形ABCD中,点A对应的复数为﹣1, ![]() 对应的复数为2+2i,
对应的复数为2+2i, ![]() 对应的复数为4﹣4i.
对应的复数为4﹣4i.
(Ⅰ)求D点对应的复数;
(Ⅱ)求平行四边形ABCD的面积.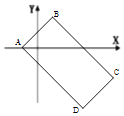
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=1﹣nan(n∈N*)
(1)计算a1 , a2 , a3 , a4;
(2)猜想an的表达式,并用数学归纳法证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为[﹣1,5],部分对应值如表,
x | ﹣1 | 0 | 4 |
f(x) | 1 | 2 | 2 |
f(x)的导函数y=f′(x)的图象(该图象关于(2,0)中心对称) 如图所示.
下列关于f(x)的命题:
①函数f(x)的极大值点为 0与4;
②函数f(x)在[0,2]上是减函数;
③函数y=f(x)﹣a零点的个数可能为0、1、2、3、4个;
④如果当时x∈[﹣1,t],f(x)的最大值是2,那么t的最大值为5;.
⑤函数f(x)的图象在a=1是上凸的
其中一定正确命题的序号是 . 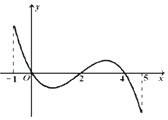
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|x﹣3|+|x﹣4|. (Ⅰ)解不等式f(x)≤2;
(Ⅱ)若对任意实数x∈[5,9],f(x)≤ax﹣1恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com