
°æƒø°ø–°√˜◊º±∏¿˚”√ ÓºŸ ±º‰»•¬√”Œ£¨¬Ë¬ËŒ™–°√˜Ã·π©Àƒ∏ˆæ∞µ„£¨æ≈’Øπµ°¢Ã©…Ω°¢≥§∞◊…Ω°¢Œ‰“ƒ…Ω£Æ–°√˜æˆ∂®”√À˘—ßµƒ ˝—ß÷™ ∂÷∆∂®“ª∏ˆ∑Ω∞∏¿¥æˆ∂®»•ƒƒ∏ˆæ∞µ„£∫£®»ÁÕº£©«˙œþ ![]() ∫Õ÷±œþ
∫Õ÷±œþ ![]() Ωª”⁄µ„
Ωª”⁄µ„ ![]() £Æ“‘
£Æ“‘ ![]() Œ™∆µ„£¨‘Ÿ¥”«˙œþ
Œ™∆µ„£¨‘Ÿ¥”«˙œþ ![]() …œ»Œ»°¡Ω∏ˆµ„∑÷±Œ™÷’µ„µ√µΩ¡Ω∏ˆœÚ¡ø£¨º«’‚¡Ω∏ˆœÚ¡øµƒ ˝¡øª˝Œ™
…œ»Œ»°¡Ω∏ˆµ„∑÷±Œ™÷’µ„µ√µΩ¡Ω∏ˆœÚ¡ø£¨º«’‚¡Ω∏ˆœÚ¡øµƒ ˝¡øª˝Œ™ ![]() £Æ»Ù
£Æ»Ù ![]() »•æ≈’Ø𵣪»Ù
»•æ≈’Ø𵣪»Ù ![]() »•Ã©…Ω£ª»Ù
»•Ã©…Ω£ª»Ù ![]() »•≥§∞◊…Ω£ª
»•≥§∞◊…Ω£ª ![]() »•Œ‰“ƒ…Ω£Æ
»•Œ‰“ƒ…Ω£Æ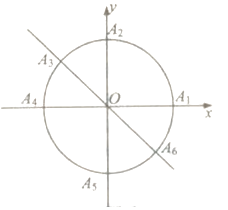
£®1£©»Ù¥” ![]() ’‚¡˘∏ˆµ„÷–»Œ»°¡Ω∏ˆµ„∑÷±Œ™÷’µ„µ√µΩ¡Ω∏ˆœÚ¡ø£¨∑÷±«Û–°√˜»•æ≈’Ø𵵃∏≈¬ ∫Õ≤ª»•Ã©…Ωµƒ∏≈¬ £ª
’‚¡˘∏ˆµ„÷–»Œ»°¡Ω∏ˆµ„∑÷±Œ™÷’µ„µ√µΩ¡Ω∏ˆœÚ¡ø£¨∑÷±«Û–°√˜»•æ≈’Ø𵵃∏≈¬ ∫Õ≤ª»•Ã©…Ωµƒ∏≈¬ £ª
£®2£©∞¥…œ ˆ∑Ω∞∏£¨–°√˜‘⁄«˙œþ ![]() …œ»°µ„
…œ»°µ„ ![]() ◊˜Œ™œÚ¡øµƒ÷’µ„£¨‘Ú–°√˜æˆ∂®»•Œ‰“ƒ…Ω£Æµ„
◊˜Œ™œÚ¡øµƒ÷’µ„£¨‘Ú–°√˜æˆ∂®»•Œ‰“ƒ…Ω£Æµ„ ![]() ‘⁄«˙œþ
‘⁄«˙œþ ![]() …œ‘À∂Ø£¨»Ùµ„
…œ‘À∂Ø£¨»Ùµ„ ![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™ ![]() £¨«Û
£¨«Û ![]() µƒ◊Ó¥Û÷µ£Æ
µƒ◊Ó¥Û÷µ£Æ
°æ¥∞∏°ø
£®1£©Ω‚£∫”…“‚ø…÷™µ√µΩœÚ¡ø◊È∫œ∑Ω Ωπ≤”–£∫
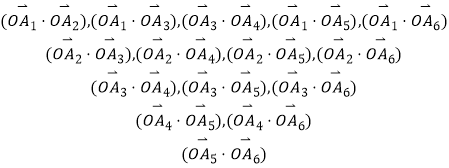
π≤15÷÷
…Ë ¬º˛°∞»•æ≈’Øπµ°±=B£¨°∞≤ª»•Ã©…Ω°±=C
‘Ú»•æ≈’Øπµº¥¶Œ>0£∫ ![]()
π≤4÷÷
![]()
»•Ã©…Ωº¥=0£¨ ![]()
π≤4÷÷
![]()
£®2£©Ω‚£∫”…“‚£∫–°√˜»•Œ‰“ƒ…Ωº¥ ![]()
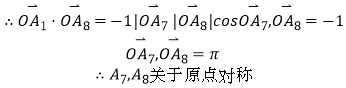
π ø……Ë ![]()
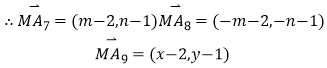
![]()
…œ Ωº∏∫Œ“‚“£∫‘≤ ![]() …œµƒµ„”ε„£®6£¨3£©µƒæý¿Î
…œµƒµ„”ε„£®6£¨3£©µƒæý¿Î
…œ Ωµƒ◊Ó¥Û÷µº¥µ„ ![]() æý¿Îµƒ◊Ó¥Û÷µ£¨º¥‘≤–ƒ
æý¿Îµƒ◊Ó¥Û÷µ£¨º¥‘≤–ƒ ![]() µƒæý¿Î‘Ÿº”∞Îæ∂
µƒæý¿Î‘Ÿº”∞Îæ∂
º¥ ![]()
À˘“‘ ![]()
°æΩ‚Œˆ°ø(1)”…“‚¡–≥ˆÀ˘”–ø…ƒÐµƒ ¬º˛Ω·∫œπ≈µ‰∏≈¬ –Õπ´ Ωø…«Ûµ√∏≈¬ °£(2)∏˘æð“‚Ω·∫œœÚ¡øµƒ ˝¡øª˝µƒ‘ÀÀ„π´ Ωø…µ√≥ˆA7,A8πÿ”⁄‘≠µ„∂‘≥∆£¨ΩË÷˙œÚ¡øµƒ◊¯±Íπÿœµø…«Ûµ√»˝∏ˆœÚ¡ø∫Õµƒƒ£≥§Œ™‘≤ x2 + y2 = 1 …œµƒµ„”ε„£®6£¨3£©µƒæý¿Î£¨”…º∏∫Œ“‚“Âø…µ√µΩ…œ Ωµƒ◊Ó¥Û÷µº¥µ„ ( x , y ) ”Î ( 6 , 3 ) æý¿Îµƒ◊Ó¥Û÷µ£¨º¥‘≤–ƒ ( 0 , 3 ) ”Î ( 6 , 3 ) µƒæý¿Î‘Ÿº”∞Îæ∂£¨¥˙»Î ˝÷µº∆À„≥ˆΩ·π˚°£
°æøºµ„æ´Œˆ°øΩ‚¥¥Àµƒπÿº¸‘⁄”⁄¿ÌΩ‚µ„∫Õ‘≤µƒ»˝÷÷Œª÷√πÿœµµƒœýπÿ÷™ ∂£¨’∆Œ’‘≤∫Õµ„µƒŒª÷√πÿœµ£∫“‘µ„P”Α≤OµƒŒ™¿˝£®…ËP «“ªµ„£¨‘ÚPO «µ„µΩ‘≤–ƒµƒæý¿Î£©£¨P‘⁄°—OÕ‚£¨PO£ær£ªP‘⁄°—O…œ£¨PO£Ωr£ªP‘⁄°—Oƒ⁄£¨PO£ºr£Æ


 ≤π≥‰œ∞ÂΩ≠À’œµ¡–¥∞∏
≤π≥‰œ∞ÂΩ≠À’œµ¡–¥∞∏ —ß¡∑øÏ≥µµ¿ø⁄À„–ƒÀ„ÀŸÀ„ÃÏÃÏ¡∑œµ¡–¥∞∏
—ß¡∑øÏ≥µµ¿ø⁄À„–ƒÀ„ÀŸÀ„ÃÏÃÏ¡∑œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø÷¥––»ÁÕºÀ˘ 浃≥ÖÚøÚÕº£¨‘Ú ‰≥ˆµƒkµƒ÷µŒ™£® £© 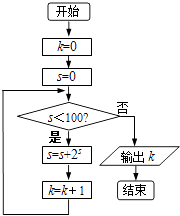
A.7
B.6
C.5
D.4
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒßΩ®“ª∏ˆ√ʪ˝Œ™360m2µƒæÿ–Œ≥°µÿ£¨“™«Ûæÿ–Œ≥°µÿµƒ“ª√Ê¿˚”√æ…«Ω£®¿˚”√æ…«Ω–ËŒ¨–Þ£©£¨∆‰À¸»˝√ÊŒß«Ω“™–¬Ω®£¨‘⁄æ…«Ωµƒ∂‘√ʵƒ–¬«Ω…œ“™¡Ù“ª∏ˆøÌ∂»Œ™2mµƒΩ¯≥ˆø⁄£¨“—÷™æ…«ΩµƒŒ¨–Þ∑—”√Œ™45‘™/m£¨–¬«Ωµƒ‘Ϻ€Œ™180‘™/m£¨…Ë¿˚”√µƒæ…«Ωµƒ≥§∂»Œ™x£®µ•Œª£∫m£©£¨–ÞΩ®¥Àæÿ–Œ≥°µÿŒß«Ωµƒ◊Ð∑—”√Œ™y£®µ•Œª£∫‘™£©£Æ £®¢Ò£©Ω´y±Ì 挙xµƒ∫Ø ˝£∫
£®¢Ú£© ‘»∑∂®x£¨ π–ÞΩ®¥Àæÿ–Œ≥°µÿŒß«Ωµƒ◊Ð∑—”√◊Ó–°£¨≤¢«Û≥ˆ◊Ó–°◊Ð∑—”√£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡Àµ√µΩ∫Ø ˝ ![]() µƒÕºœÛ£¨ø…“‘Ω´∫Ø ˝
µƒÕºœÛ£¨ø…“‘Ω´∫Ø ˝ ![]() µƒÕºœÛ£® £©
µƒÕºœÛ£® £©
A.œÚ”“∆Ω“∆ ![]() ∏ˆµ•Œª
∏ˆµ•Œª
B.œÚ◊Û∆Ω“∆ ![]() ∏ˆµ•Œª
∏ˆµ•Œª
C.œÚ”“∆Ω“∆ ![]() ∏ˆµ•Œª
∏ˆµ•Œª
D.œÚ◊Û∆Ω“∆ ![]() ∏ˆµ•Œª
∏ˆµ•Œª
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™ ˝¡–{an}£¨{bn}¬˙◊„a1=1£¨a2=2£¨b1=2£¨«“∂‘»Œ“‚µƒ’˝’˚ ˝i£¨j£¨k£¨l£¨µ±i+j=k+l ±£¨∂º”–ai+bj=ak+bl £¨ ‘Ú ![]() µƒ÷µ «£® £©
µƒ÷µ «£® £©
A.2012
B.2013
C.2014
D.2015
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™œÚ¡ø ![]() £¨º«∫Ø ˝
£¨º«∫Ø ˝ ![]() .«Û£∫
.«Û£∫
£®I£©∫Ø ˝ ![]() µƒ◊Ó–°÷µº∞»°µ√◊Ó–°÷µ ±
µƒ◊Ó–°÷µº∞»°µ√◊Ó–°÷µ ± ![]() µƒºØ∫œ£ª
µƒºØ∫œ£ª
£®II£©«Û∫Ø ˝f(x) µƒµ•µ˜‘ˆ«¯º‰°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™¡ΩÃı÷±œþ ![]() £¨¡Ω∏ˆ∆Ω√Ê
£¨¡Ω∏ˆ∆Ω√Ê ![]() £¨∏¯≥ˆœ¬√ÊÀƒ∏ˆ√¸Ã‚£∫
£¨∏¯≥ˆœ¬√ÊÀƒ∏ˆ√¸Ã‚£∫
¢Ÿ ![]() £¨
£¨ ![]() £ª¢⁄
£ª¢⁄ ![]() £¨
£¨ ![]() £¨
£¨ ![]() £ª
£ª
¢€ ![]() £¨
£¨ ![]() £ª¢Ð
£ª¢Ð ![]() £¨
£¨ ![]() £¨
£¨ ![]()
∆‰÷–’˝»∑√¸Ã‚µƒ–Ú∫≈ «£® £©
A.¢Ÿ¢Ð
B.¢⁄¢Ð
C.¢Ÿ¢€
D.¢⁄¢€
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øF1 £¨ F2∑÷± «À´«˙œþ ![]() ©Å
©Å ![]() =1£®a£¨b£æ0£©µƒ◊Û”“Ω𵄣¨µ„P‘⁄À´«˙œþ…œ£¨¬˙◊„
=1£®a£¨b£æ0£©µƒ◊Û”“Ω𵄣¨µ„P‘⁄À´«˙œþ…œ£¨¬˙◊„ ![]() =0£¨»Ù°˜PF1F2µƒƒ⁄«–‘≤∞Îæ∂”ÎÕ‚Ω”‘≤∞Îæ∂÷Ʊ»Œ™
=0£¨»Ù°˜PF1F2µƒƒ⁄«–‘≤∞Îæ∂”ÎÕ‚Ω”‘≤∞Îæ∂÷Ʊ»Œ™ ![]() £¨‘Ú∏√À´«˙œþµƒ¿Î–ƒ¬ Œ™£® £©
£¨‘Ú∏√À´«˙œþµƒ¿Î–ƒ¬ Œ™£® £©
A.![]()
B.![]()
C.![]() +1
+1
D.![]() +1
+1
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©=sin£®2x+¶’1£©£¨g£®x£©=cos£®4x+¶’2£©£¨|¶’1|°Ð ![]() £¨|¶’2|°Ð
£¨|¶’2|°Ð ![]() £Æ √¸Ã‚¢Ÿ£∫»Ù÷±œþx=¶’ «∫Ø ˝f£®x£©∫Õg£®x£©µƒ∂‘≥∆÷·£¨‘Ú÷±œþx=
£Æ √¸Ã‚¢Ÿ£∫»Ù÷±œþx=¶’ «∫Ø ˝f£®x£©∫Õg£®x£©µƒ∂‘≥∆÷·£¨‘Ú÷±œþx= ![]() k¶–+¶’£®k° Z£© «∫Ø ˝g£®x£©µƒ∂‘≥∆÷·£ª
k¶–+¶’£®k° Z£© «∫Ø ˝g£®x£©µƒ∂‘≥∆÷·£ª
√¸Ã‚¢⁄£∫»Ùµ„P£®¶’£¨0£© «∫Ø ˝f£®x£©∫Õg£®x£©µƒ∂‘≥∆÷––ƒ£¨‘Úµ„Q£® ![]() +¶’£¨0£©£®k° Z£© «∫Ø ˝f£®x£©µƒ÷––ƒ∂‘≥∆£Æ£® £©
+¶’£¨0£©£®k° Z£© «∫Ø ˝f£®x£©µƒ÷––ƒ∂‘≥∆£Æ£® £©
A.√¸Ã‚¢Ÿ¢⁄∂º’˝»∑
B.√¸Ã‚¢Ÿ¢⁄∂º≤ª’˝»∑
C.√¸Ã‚¢Ÿ’˝»∑£¨√¸Ã‚¢⁄≤ª’˝»∑
D.√¸Ã‚¢Ÿ≤ª’˝»∑£¨√¸Ã‚¢⁄’˝»∑
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com