
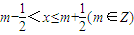 ,则m叫做离实数x最近的整数,记作{x},即{x}=m.在此基础上有函数f(x)=|x-{x}|(x∈R).对于函数f(x)给出如下判断.
,则m叫做离实数x最近的整数,记作{x},即{x}=m.在此基础上有函数f(x)=|x-{x}|(x∈R).对于函数f(x)给出如下判断.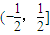 上单调递增;
上单调递增;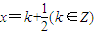 对称;⑤函数y=f(x)的图象关于直线x=k(k∈Z)对称.
对称;⑤函数y=f(x)的图象关于直线x=k(k∈Z)对称.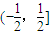 上不是单调递增.④⑤利用若函数满足f(a-x)=f(x),则函数对称轴为x=
上不是单调递增.④⑤利用若函数满足f(a-x)=f(x),则函数对称轴为x=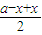 ,来判断函数的对称性.
,来判断函数的对称性.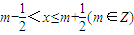 ,∴
,∴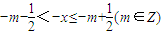
 ,∴
,∴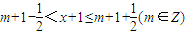
 ∈
∈ ,
, ∈
∈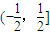 ,且{
,且{ }=0,{
}=0,{ }=0
}=0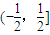 上单调递增,∴③错误
上单调递增,∴③错误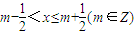 ,∴
,∴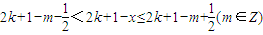
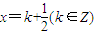 对称
对称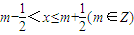 ,∴
,∴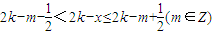


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:单选题
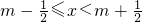 (其中m为整数),则m叫离实数x最近的整数,记作[x]=m,已知f(x)=|[x]-x|,下列四个命题:
(其中m为整数),则m叫离实数x最近的整数,记作[x]=m,已知f(x)=|[x]-x|,下列四个命题: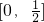 ; ②函数f(x)是R上的增函数;
; ②函数f(x)是R上的增函数;查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市海淀区八一中学高三(上)周练数学试卷(2)(理科)(解析版) 题型:选择题
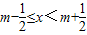 (其中m为整数),则m叫离实数x最近的整数,记作[x]=m,已知f(x)=|[x]-x|,下列四个命题:
(其中m为整数),则m叫离实数x最近的整数,记作[x]=m,已知f(x)=|[x]-x|,下列四个命题: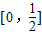 ; ②函数f(x)是R上的增函数;
; ②函数f(x)是R上的增函数;查看答案和解析>>
科目:高中数学 来源:2012年北京市门头沟区高考数学一模试卷(文科)(解析版) 题型:选择题
 (其中m为整数),则m叫离实数x最近的整数,记作[x]=m,已知f(x)=|[x]-x|,下列四个命题:
(其中m为整数),则m叫离实数x最近的整数,记作[x]=m,已知f(x)=|[x]-x|,下列四个命题: ; ②函数f(x)是R上的增函数;
; ②函数f(x)是R上的增函数;查看答案和解析>>
科目:高中数学 来源:2012年北京市门头沟区高考数学一模试卷(理科)(解析版) 题型:解答题
 (其中m为整数),则m叫离实数x最近的整数,记作[x]=m,已知f(x)=|[x]-x|,下列四个命题:
(其中m为整数),则m叫离实数x最近的整数,记作[x]=m,已知f(x)=|[x]-x|,下列四个命题: ; ②函数f(x)是R上的增函数;
; ②函数f(x)是R上的增函数;查看答案和解析>>
科目:高中数学 来源:北京模拟题 题型:填空题
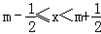 (其中m为整数),则m叫离实数x最近的整数,记作[x]=m,已知f(x)=|[x]﹣x|,下列四个命题:
(其中m为整数),则m叫离实数x最近的整数,记作[x]=m,已知f(x)=|[x]﹣x|,下列四个命题: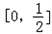 ;
; 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com