
【题目】已知一个口袋有![]() 个白球,
个白球,![]() 个黑球,这些球除颜色外全部相同,现将口袋中的球随机逐个取出,并依次放入编号为
个黑球,这些球除颜色外全部相同,现将口袋中的球随机逐个取出,并依次放入编号为![]() ,
,![]() ,
,![]() ,
,![]() 的抽屉内.
的抽屉内.
(1)求编号为![]() 的抽屉内放黑球的概率;
的抽屉内放黑球的概率;
(2)口袋中的球放入抽屉后,随机取出两个抽屉中的球,求取出的两个球是一黑一白的概率.
【答案】(1) ![]() .(2)
.(2) ![]() .
.
【解析】
(1)4个球放入编号为1,2,3,4的抽屉里,有4种方法,满足题意的有1中,根据古典概型公式得到结果;(2)根据抽屉的编号,对于一种确定的放法,取法有6种情况,满足一白一黑的有3种情况,进而得到结果.
(1)将口袋中的![]() 个白球,
个白球,![]() 个黑球,依次放入编号为
个黑球,依次放入编号为![]() ,
,![]() ,
,![]() ,
,![]() 的抽屉内,共有
的抽屉内,共有![]() 种不同的放法,分别是(白,白,白,黑),(白,白,黑,白),(白,黑,白,白),(黑,白,白,白),其中编号为
种不同的放法,分别是(白,白,白,黑),(白,白,黑,白),(白,黑,白,白),(黑,白,白,白),其中编号为![]() 的抽屉内放黑球的情况有
的抽屉内放黑球的情况有![]() 种,所以编号为
种,所以编号为![]() 的抽屉内放黑球的概率为
的抽屉内放黑球的概率为![]() .
.
(2)假设口袋内的球逐个依次取出放入抽屉内后是(白,白,白,黑),随机取出两个球,根据抽屉的编号,可能是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共6种,其中一黑一白的是
共6种,其中一黑一白的是![]() ,
,![]() ,
,![]() 共
共![]() 种,所以取出的两个球是一黑一白的概率为
种,所以取出的两个球是一黑一白的概率为![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在平行四边形![]() 中,
中,![]() 点
点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]()
(1)求证; 平面![]() 平面
平面![]() ;
;
(2)若平面![]() 和平面
和平面![]() 的交线为
的交线为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】出租车几何学是由十九世纪的赫尔曼·闵可夫斯基所创立的。在出租车几何学中,点还是形如![]() 的有序实数对,直线还是满足
的有序实数对,直线还是满足![]() 的所有
的所有![]() 组成的图形,角度大小的定义也和原来一样,直角坐标系内任意两点
组成的图形,角度大小的定义也和原来一样,直角坐标系内任意两点![]() 定义它们之间的一种“距离”:
定义它们之间的一种“距离”:![]() ,请解决以下问题:
,请解决以下问题:
(1)求线段![]() 上一点
上一点![]() 到点
到点![]() 的“距离”;
的“距离”;
(2)定义:“圆”是所有到定点“距离”为定值的点组成的图形,求“圆”上的所有点到点![]() 的“距离”均为
的“距离”均为![]() 的“圆”方程,并求该“圆”围成的图形的面积;
的“圆”方程,并求该“圆”围成的图形的面积;
(3)若点![]() 到点
到点![]() 的“距离”和点
的“距离”和点![]() 到点
到点![]() 的“距离”相等,其中实数
的“距离”相等,其中实数![]() 满足
满足![]() ,求所有满足条件的点
,求所有满足条件的点![]() 的轨迹的长之和.
的轨迹的长之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的普及,大学生迷恋手机的现象非常严重.为了调查双休日大学生使用手机的时间,某机构采用不记名方式随机调查了使用手机时间不超过![]() 小时的
小时的![]() 名大学生,将
名大学生,将![]() 人使用手机的时间分成
人使用手机的时间分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别加以统计,得到下表,根据数据完成下列问题:
分别加以统计,得到下表,根据数据完成下列问题:
使用时间/时 |
|
|
|
|
|
大学生/人 |
|
|
|
|
|

(1)完成频率分布直方图;
(2)根据频率分布直方图估计大学生使用手机的平均时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
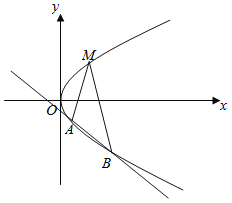
【题目】如图所示,已知点![]() 是抛物线
是抛物线![]() 上一定点,直线
上一定点,直线![]() 的倾斜角互补,且与抛物线另交于
的倾斜角互补,且与抛物线另交于![]() ,
,![]() 两个不同的点.
两个不同的点.
(1)求点![]() 到其准线的距离;
到其准线的距离;
(2)求证:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
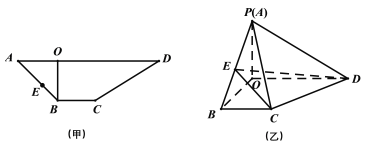
【题目】如图甲所示,![]() 是梯形
是梯形![]() 的高,
的高,![]() ,
,![]() ,
,![]() ,先将梯形
,先将梯形![]() 沿
沿![]() 折起如图乙所示的四棱锥
折起如图乙所示的四棱锥![]() ,使得
,使得![]() .
.
(1)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请求出
?若存在,请求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)点![]() 是线段
是线段![]() 上一动点,当直线
上一动点,当直线![]() 与
与![]() 所成的角最小时,求二面角
所成的角最小时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com