
分析 (1)求出函数的导数,求出斜率与切点坐标,然后求解切线方程.
(2)求出函数的定义域,求出导数,通过当k≥0时,①当-4≤k<0时,②当k<-4时,判断导函数的符号,求出函数的单调区间.
(3)推出$h(x)=2xlnx-\frac{1}{3}{x^3}+k{x^2}$,求解定义域与导数,利用h(x)在定义域内单调减,得到$2k≤\frac{{{x^2}-2lnx-2}}{x}$在(0,+∞)恒成立,构造$s(x)=\frac{{{x^2}-2lnx-2}}{x}=x-\frac{2lnx}{x}-\frac{2}{x}$,求出导函数,记t(x)=x2+2lnx,判断导函数的符号,利用所以存在唯一的${x_0}∈(\frac{{\sqrt{2}}}{2},1)$,求出s(x)取得极小值,且是最小值.然后求解k的最大值.
解答 解:(1)$f(x)=2lnx-\frac{1}{3}{x^2}+\frac{2}{3}x$,则$f'(x)=\frac{2}{x}-\frac{2}{3}x+\frac{2}{3}$,…(1分)
则f′(1)=2,又$f(1)=\frac{1}{3}$,
所以函数y=f(x)的图象在x=1处的切线方程为$y-\frac{1}{3}=2(x-1)$,
即$y=2x-\frac{5}{3}$. …(3分)
(2)g(x)=2lnx+x2+kx,定义域为(0,+∞),…(4分)
则$g'(x)=\frac{2}{x}+2x+k=\frac{{2{x^2}+kx+2}}{x}$,
当k≥0时,显然g′(x)>0恒成立,此时g(x)在(0,+∞)单调增; …(6分)
当k<0时,2x2+kx+2=0(*),△=k2-16,
①当-4≤k<0时,g′(x)≥0恒成立,此时g(x)在(0,+∞)单调增; …(7分)
②当k<-4时,方程(*)有两个不等的实数根${x_1}=\frac{{-k+\sqrt{{k^2}-16}}}{4}>{x_2}=\frac{{-k-\sqrt{{k^2}-16}}}{4}>0$
所以g(x)在(0,x2)上单调增,在(x2,x1)上单调减,在(x1,+∞)上单调增,
综上,当k≥-4时,g(x)在(0,+∞)单调增;
当k<-4时,g(x)在(0,x2)上单调增,在(x2,x1)上单调减,在(x1,+∞)上单调增.
…(9分)
(3)$h(x)=2xlnx-\frac{1}{3}{x^3}+k{x^2}$,定义域为(0,+∞),则h′(x)=2(lnx+1)-x2+2kx.
因为h(x)在定义域内单调减,所以h′(x)≤0在(0,+∞)恒成立,
即$2k≤\frac{{{x^2}-2lnx-2}}{x}$在(0,+∞)恒成立,即$2k≤{(\frac{{{x^2}-2lnx-2}}{x})_{min}}$…(11分)
令$s(x)=\frac{{{x^2}-2lnx-2}}{x}=x-\frac{2lnx}{x}-\frac{2}{x}$,则$s'(x)=1-\frac{2-2lnx}{x^2}+\frac{2}{x^2}=\frac{{{x^2}+2lnx}}{x^2}$,
记t(x)=x2+2lnx,则$t'(x)=2x+\frac{2}{x}>0(x>0)$,所以t(x)在(0,+∞)单调增,且$t(\frac{{\sqrt{2}}}{2})=\frac{1}{2}+2ln\frac{{\sqrt{2}}}{2}=\frac{1}{2}-ln2<0$,k(1)=1>0,
所以存在唯一的${x_0}∈(\frac{{\sqrt{2}}}{2},1)$,$s'({x_0})=\frac{{x_0^2+2ln{x_0}}}{x_0^2}=0$,有$2ln{x_0}=-x_0^2$,…(13分)
此时,当x∈(0,x0)时,s′(x)<0,当x∈(x0,+∞)时,s′(x)>0,
所以,当x=x0时,s(x)取得极小值,且是最小值.
所以$2k≤s{(x)_{min}}=\frac{{x_0^2-2ln{x_0}-2}}{x_0}=\frac{2x_0^2-2}{x_0}$,即$k≤{x_0}-\frac{1}{x_0}$,…(15分)
又${x_0}∈(\frac{{\sqrt{2}}}{2},1)$,所以${x_0}-\frac{1}{x_0}∈(-\frac{{\sqrt{2}}}{2},0)$,
因为k∈Z,则k的最大值为-1. …(16分)
点评 本题考查函数的导数的综合应用,函数的单调性以及函数的极值以及函数的最值的求法,考查构造法的应用地产股涨幅以及导数的应用,难度大,需要解题仔细认真,考查分类讨论,转化思想的应用.


科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,都有$x_{\;}^2+2x+5≠0$ | B. | ?x∈R,都有$x_{\;}^2+2x+5=0$ | ||
| C. | ?x0∈R,都有$x_0^2+2{x_0}+5≠0$ | D. | ?x∉R,都有$x_{\;}^2+2x+5≠0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
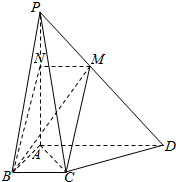 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{3}$AD,过BC的平面交PD于M,交PA于N(N与A不重合).
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{3}$AD,过BC的平面交PD于M,交PA于N(N与A不重合).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$•$\overrightarrow{{A}_{1}{C}_{1}}$=a2 | B. | $\overrightarrow{A{C}_{1}}$•$\overrightarrow{B{D}_{1}}$=0 | C. | $\overrightarrow{AB}$•$\overrightarrow{A{C}_{1}}$=$\sqrt{2}$a2 | D. | $\overrightarrow{BC}$•$\overrightarrow{D{A}_{1}}$=a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2ex-e-1 | B. | y=2ex-e+1 | C. | y=2ex+e-1 | D. | y=2ex+e+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com