
【题目】函数f(x)=sin2x+2 ![]() cos2x﹣
cos2x﹣ ![]() ,函数g(x)=mcos(2x﹣
,函数g(x)=mcos(2x﹣ ![]() )﹣2m+3(m>0),若存在x1 , x2∈[0,
)﹣2m+3(m>0),若存在x1 , x2∈[0, ![]() ],使得f(x1)=g(x2)成立,则实数m的取值范围是( )
],使得f(x1)=g(x2)成立,则实数m的取值范围是( )
A.(0,1]
B.[1,2]
C.[ ![]() ,2]
,2]
D.[ ![]() ,
, ![]() ]
]
 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】己知直线2x﹣y﹣4=0与直线x﹣2y+1=0交于点p.
(1)求过点p且垂直于直线3x+4y﹣15=0的直线l1的方程;(结果写成直线方程的一般式)
(2)求过点P并且在两坐标轴上截距相等的直线l2方程(结果写成直线方程的一般式)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每公里的费用总和最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
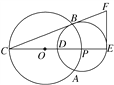
【题目】如图,圆O与圆P相交于A,B两点,圆心P在圆O上,圆O的弦BC切圆P于点B,CP及其延长线交圆P于D,E两点,过点E作EF⊥CE,交CB的延长线于点F.
(1)求证:B,P,E,F四点共圆;
(2)若CD=2,CB=2![]() ,求出由B,P,E,F四点所确定的圆的直径.
,求出由B,P,E,F四点所确定的圆的直径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B,C,D为平面内的四点,且A(1,3),B(2,﹣2),C(4,1).
(1)若 ![]() =
= ![]() ,求D点的坐标;
,求D点的坐标;
(2)设向量 ![]() =
= ![]() ,
, ![]() =
= ![]() ,若k
,若k ![]() ﹣
﹣ ![]() 与
与 ![]() +3
+3 ![]() 平行,求实数k的值.
平行,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】漳州市“网约车”的现行计价标准是:路程在2km以内(含2km)按起步价8元收取,超过2km后的路程按1.9元/km收取,但超过10km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85元).
(1)将某乘客搭乘一次“网约车”的费用f(x)(单位:元)表示为行程x(0<x≤60,单位:km)的分段函数;
(2)某乘客的行程为16km,他准备先乘一辆“网约车”行驶8km后,再换乘另一辆“网约车”完成余下行程,请问:他这样做是否比只乘一辆“网约车”完成全部行程更省钱?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=﹣ ![]() x3+x2+(m2﹣1)x,(x∈R),其中m>0.
x3+x2+(m2﹣1)x,(x∈R),其中m>0.
(1)当m=1时,曲线y=f(x)在点(1,f(1))处的切线斜率;
(2)求函数的单调区间与极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com