
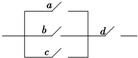
 [文]如图所示,a,b,c,d是四处处于断开状态的开关,任意将其中两个闭合,则电路被接通的概率为.
[文]如图所示,a,b,c,d是四处处于断开状态的开关,任意将其中两个闭合,则电路被接通的概率为. | 3 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
 (文)如图所示:已知椭圆C:
(文)如图所示:已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| |PF1| |
| 1 |
| |QF| |
| AP |
| AQ |
| 4 |
| 3 |
| 9 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年湖南卷文)如图所示,四棱锥![]() 的底面
的底面![]() 是边长为1的菱形,
是边长为1的菱形,![]() ,E是CD的中点,PA
,E是CD的中点,PA![]() 底面ABCD,
底面ABCD,![]() 。
。
(1)证明:平面PBE![]() 平面PAB;
平面PAB;
(2)求二面角A―BE―P和的大小。

查看答案和解析>>
科目:高中数学 来源:2008-2009学年重庆市渝中区巴蜀中学高三(上)月考数学试卷(文理合卷)(解析版) 题型:解答题
 ,F1、F2为其左、右焦点,A为右顶点,过F1的直线l与椭圆相交于P、Q两点,且有
,F1、F2为其左、右焦点,A为右顶点,过F1的直线l与椭圆相交于P、Q两点,且有 .
. ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com