
【题目】某校为研究学生语言学科的学习情况,现对高二200名学生英语和语文某次考试成绩进行抽样分析.将200名学生编号为001,002,…,200,采用系统抽样的方法等距抽取10名学生,将10名学生的两科成绩(单位:分)绘成折线图如下: 
(Ⅰ)若第一段抽取的学生编号是006,写出第五段抽取的学生编号;
(Ⅱ)在这两科成绩差超过20分的学生中随机抽取2人进行访谈,求2人成绩均是语文成绩高于英语成绩的概率;
(Ⅲ)根据折线图,比较该校高二年级学生的语文和英语两科成绩,写出你的结论和理由.
【答案】解:(Ⅰ)第一段抽取的学生编号是006,间隔为20,第五段抽取的学生编号为086;
(Ⅱ)这两科成绩差超过20分的学生,共5人,语文成绩高于英语成绩,有3人,从中随机抽取2人进行访谈,有 ![]() =10种,2人成绩均是语文成绩高于英语成绩,有3种,故2人成绩均是语文成绩高于英语成绩的概率是
=10种,2人成绩均是语文成绩高于英语成绩,有3种,故2人成绩均是语文成绩高于英语成绩的概率是 ![]() ;
;
(Ⅲ)根据折线图,可以估计该校高二年级学生的语文成绩平均分高,语文成绩相对更稳定
【解析】(Ⅰ)第一段抽取的学生编号是006,间隔为20,即可写出第五段抽取的学生编号;(Ⅱ)确定基本事件的个数,可得结论;(Ⅲ)根据折线图,可以估计该校高二年级学生的语文成绩平均分高,语文成绩相对更稳定.
【考点精析】解答此题的关键在于理解系统抽样方法的相关知识,掌握把总体的单位进行排序,再计算出抽样距离,然后按照这一固定的抽样距离抽取样本;第一个样本采用简单随机抽样的办法抽取.


科目:高中数学 来源: 题型:
【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
B餐厅分数频数分布表 | |
分数区间 | 频数 |
[0,10) | 2 |
[10,20) | 3 |
[20,30) | 5 |
[30,40) | 15 |
[40,50) | 40 |
[50,60] | 35 |
定义学生对餐厅评价的“满意度指数”如下:
分数 | [0,30) | [30,50) | [50,60] |
满意度指数 | 0 | 1 | 2 |

(Ⅰ)在抽样的100人中,求对A餐厅评价“满意度指数”为0的人数;
(Ⅱ)从该校在A,B两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,0<φ<π),其导函数f′(x)的部分图象如图所示,则函数f(x)的解析式为( )
A.f(x)=4sin( ![]() x+
x+ ![]() π)
π)
B.f(x)=4sin( ![]() x+
x+ ![]() )
)
C.f(x)=4sin( ![]() x+
x+ ![]() )
)
D.f(x)=4sin( ![]() x+
x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆G: ![]() 的两个焦点分别为F1和F2 , 短轴的两个端点分别为B1和B2 , 点P在椭圆G上,且满足|PB1|+|PB2|=|PF1|+|PF2|.当b变化时,给出下列三个命题: ①点P的轨迹关于y轴对称;
的两个焦点分别为F1和F2 , 短轴的两个端点分别为B1和B2 , 点P在椭圆G上,且满足|PB1|+|PB2|=|PF1|+|PF2|.当b变化时,给出下列三个命题: ①点P的轨迹关于y轴对称;
②存在b使得椭圆G上满足条件的点P仅有两个;
③|OP|的最小值为2,
其中,所有正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 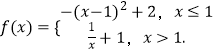 下列四个命题: ①f(f(1))>f(3);
下列四个命题: ①f(f(1))>f(3);
②x0∈(1,+∞), ![]() ;
;
③f(x)的极大值点为x=1;
④x1 , x2∈(0,+∞),|f(x1)﹣f(x2)|≤1
其中正确的有 . (写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高一、高二年级各有8个班,学校调查了春学期各班的文学名著阅读量(单位:本),并根据调查结果,得到如下所示的茎叶图: 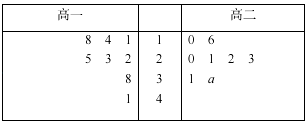
为鼓励学生阅读,在高一、高二两个两个年级中,学校将阅读量高于本年级阅读量平均数的班级命名为该年级的“书香班级”.
(1)当a=4时,记高一年级“书香班级”数为m,高二年级的“书香班级”数为n,比较m,n的大小关系;
(2)在高一年级8个班级中,任意选取两个,求这两个班级均是“书香班级”的概率;
(3)若高二年级的“书香班级”数多于高一年级的“书香班级”数,求a的值(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( ) 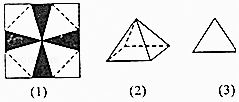
A.![]() cm3
cm3
B.![]() cm3
cm3
C.![]() cm3
cm3
D.![]() cm3
cm3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(3+x)﹣log2(3﹣x),
(1)求函数f(x)的定义域,并判断函数f(x)的奇偶性;
(2)已知f(sinα)=1,求α的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com