Question

【题目】在边长为2的菱形中，，将菱形沿对角线折起，使二面角的大小为，则所得三棱锥的外接球表面积为（ ）

A.B.C.D.

Answer 1

【答案】B

【解析】

由已知可得、都是边长为的等边三角形，由菱形的对角线互相垂直，可得为二面角的平面角，即，作出图形，找出三棱锥的外接球球心，利用四点共圆结合正弦定理求解三棱锥的外接球的半径，代入球的表面积公式可得结果.

由于四边形是边长为的菱形，且，则，

所以，、都是边长为的等边三角形，

由于菱形的对角线互相垂直，则，，

所以，为二面角的平面角，即，

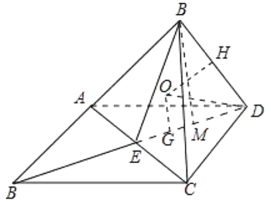
过点作平面的垂线，垂足为点，则点在线段上，

由，，可得，

且是等边三角形，所以，，

设的外心为点，的中点，

在平面内，过点、分别作平面、的垂线交于点，

则点为三棱锥的外接球的球心，则，，

，则，

由于、、、四点共圆，可得，

所以，三棱锥的外接球的表面积为.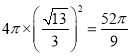

故选：B.