
【题目】如图,已知四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 为
为![]() 上任意一点,
上任意一点,![]() 为菱形
为菱形![]() 对角线的交点。
对角线的交点。
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,当四棱锥的体积被平面
,当四棱锥的体积被平面![]() 分成3:1两部分时,若二面角
分成3:1两部分时,若二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值。
的值。

【答案】(1)见解析(2)![]()
【解析】
(1)通过在面内作交线的垂线,和面面垂直性质定理证明![]() 面ABCD,再通过
面ABCD,再通过![]() 面PDB,证明平面
面PDB,证明平面![]() 平面
平面![]() 。(2)设三棱锥
。(2)设三棱锥![]() 的高为
的高为![]() ,由体积比可得
,由体积比可得![]() ,故此时
,故此时![]() 为
为![]() 的中点。可证面
的中点。可证面![]() 面
面![]() 。过点
。过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() ,故
,故![]() 即为二面角
即为二面角![]() 的平面角,即
的平面角,即![]() 。进一步求的
。进一步求的![]() 的值。方法二是利用空量向量求得比值。
的值。方法二是利用空量向量求得比值。
(1)过点![]() 作
作![]() 于点G,由于平面
于点G,由于平面![]() 面
面![]() ,所以
,所以![]() 面
面![]()
![]() 面
面![]() ,故
,故![]() ;同理,过点
;同理,过点![]() 作
作![]() 于
于![]() ,则
,则![]()
![]() 面
面![]() ,
,![]() 面
面![]() ,且
,且![]()
所以![]() 面ABCD。所以
面ABCD。所以![]() ,又
,又![]() ,
,
故![]() 面
面![]() ,所以面
,所以面![]() 面面
面面![]() 。
。
(2)若四棱锥的体积被面![]() 分成3:1两部分,则
分成3:1两部分,则![]() 的体积是整个四棱锥体积的
的体积是整个四棱锥体积的![]() ,设三棱锥
,设三棱锥![]() 的高为
的高为![]() ,则
,则![]() (
(![]() 为菱形
为菱形![]() 的面积),所以
的面积),所以![]() ,故此时
,故此时![]() 为
为![]() 的中点,此时
的中点,此时![]() ,并且
,并且![]() ,故面
,故面![]() 面
面![]() ,故
,故![]() 面
面![]() ,
,![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() 面
面![]() ,连接
,连接![]() ,则
,则![]() ,故
,故![]() 即为二面角
即为二面角![]() 的平面角,即
的平面角,即![]()

设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,故
,故![]() ,
,![]()
可解得![]() ,故
,故![]()
解法二:如图建立坐标系,设![]() 则
则![]() ,设
,设![]()
则![]()
面![]() 的法向量为
的法向量为![]() ,设面面
,设面面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,取
,取![]() ,则
,则
![]()
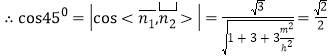
![]()


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】全国糖酒商品交易会将在四川举办.展馆附近一家川菜特色餐厅为了研究参会人数与本店所需原材料数量的关系,在交易会前查阅了最近5次交易会的参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下数据:
(袋),得到如下数据:
举办次数 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
参会人数 | 11 | 9 | 8 | 10 | 12 |
原材料 | 28 | 23 | 20 | 25 | 29 |
(Ⅰ)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)若该店现有原材料12袋,据悉本次交易会大约有13万人参加,为了保证原材料能够满足需要,则该店应至少再补充原材料多少袋?
(参考公式: ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个文艺比赛中,12名专业人士和12名观众代表各组成一个评委小组,给参赛选手打分,下面是两组评委对同一名选手的打分:
小组A 42 45 48 46 52 47 49 55 42 51 47 45
小组B 55 36 70 66 75 49 46 68 42 62 58 47
(1)选择一个可以度量每一组评委打分相似性的量,并对每组评委的打分计算度量值.
(2)你能据此判断小组A和小组B中哪一个更像是由专业人土组成的吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆的短轴端点与双曲线
,椭圆的短轴端点与双曲线![]() 的焦点重合,过点
的焦点重合,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若以![]() 为直径的圆过坐标原点
为直径的圆过坐标原点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,抛物线的焦点
,抛物线的焦点![]() ,以
,以![]() 为焦点,离心率
为焦点,离心率![]() 的椭圆与抛物线的一个交点为
的椭圆与抛物线的一个交点为 ;自
;自![]() 引直线交抛物线于
引直线交抛物线于![]() 两个不同的点,设
两个不同的点,设![]() .
.
(1)求抛物线的方程椭圆的方程;
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 与
与![]() (
(![]() 为常数)的图象在它们与坐标轴交点处的切线互相平行.
为常数)的图象在它们与坐标轴交点处的切线互相平行.
(1)若关于![]() 的不等式
的不等式![]() 有解,求实数
有解,求实数![]() 的取值范围;
的取值范围;
(2)对于函数![]() 和
和![]() 公共定义域内的任意实数
公共定义域内的任意实数![]() ,我们把
,我们把![]() 的值称为两函数在
的值称为两函数在![]() 处的“瞬间距离”.则函数
处的“瞬间距离”.则函数![]() 与
与![]() 的所有“瞬间距离”是否都大于2?请加以证明.
的所有“瞬间距离”是否都大于2?请加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com