已知函数f(x)=ax3+bx2+cx在点x0处取得极小值-4,若f′(x)>0的x的取值范围为(1,3).
(Ⅰ)求f(x)的解析式及f(x)的极大值;
(Ⅱ)设g(x)=6(2-m)x,当x∈[2,3]时,函数y=f′(x)的图象恒在y=g(x)的图象的下方,求m的取值范围.
解:(Ⅰ)求导函数可得f′(x)=3ax
2+2bx+c,依题意有a>0,且1,3分别为f(x)的极小值,极大值点,
∴f′(1)=0,f′(3)=0,f(1)=-4
∴
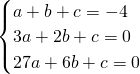
,解得a=-1,b=6,c=-9,
∴f(x)=-x
3+6x
2-9x,
∴f(x)的极大值为f(3)=0;
(Ⅱ)∵当x∈[2,3]时,函数y=f′(x)的图象恒在y=g(x)的图象的下方,
∴-3x
2+12x-9<6(2-m)x,
∴6(2-m)>-3(
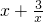
)+12,
设y=
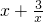
,则y′=

,∴y=
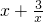
在[2,3]上是增函数,∴
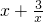
≥

∴-3(
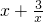
)+12≤

∴6(2-m)>

∴m<

.
分析:(Ⅰ)导数f′(x)>0的x的取值范围(1,3)得到1和3分别为函数的极小值和极大值点即f′(1)=0且f′(3)=0,且有f(1)=-4,三者联立即可求出a、b和c的值,得到f(x)的解析式,从而可得f(x)的极大值;
(Ⅱ)当x∈[2,3]时,函数y=f′(x)的图象恒在y=g(x)的图象的下方,等价于-3x
2+12x-9<6(2-m)x,分离参数,再求最值,即可求m的取值范围.
点评:本题考查导数知识的运用,考查函数的极值,考查恒成立问题,正确分离参数求最值是关键.

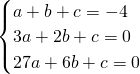 ,解得a=-1,b=6,c=-9,
,解得a=-1,b=6,c=-9,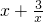 )+12,
)+12,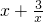 ,则y′=
,则y′= ,∴y=
,∴y=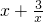 在[2,3]上是增函数,∴
在[2,3]上是增函数,∴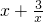 ≥
≥
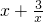 )+12≤
)+12≤

 .
.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案