口袋里装有大小相同的4个红球和8个白球,甲、乙两人依规则从袋中有放回地摸球,每次摸出一个,规则如下:①若一方摸出一个红球,则此人继续进行下一次摸球;若一方摸出一个白球,则改换为由对方进行下一次摸球;②每一个摸球彼此相互独立,并约定由甲开始进行第一次摸球,求在前三次的摸球中:
(1)乙恰好摸到一个红球的概率;
(2)甲至少摸到一个红球的概率;
(3)甲摸到红球的次数ξ的分布列及数学期望.
分析:(1)乙恰好摸到一个红球包括两种情况,甲第一次摸到一个红球,第二次没有摸到红球改为乙摸球,且摸到一个红球;二是甲第一次摸球,摸到一个白球,乙开始摸球摸到一个红球,乙接着摸球,摸到一个白球.根据相互独立事件同时发生的概率写出结果.
(2)甲至少摸到一个红球的对立事件是甲在前三次摸球中没有摸到红球,算出甲在前三次摸球中,没有摸到红球的概率,根据对立事件的概率公式得到甲至少摸到一个红球的概率.
(3)甲摸到红球的次数为ξ,根据题意知ξ的可能取值为0,1,2,3,结合变量对应的事件写出变量的分布列,算出期望.
解答:解:记“甲摸球一次摸出红球”为事件A“乙摸球一次摸出红球”为事件B,
则
P(A)=P(B)==,
P()=P()=且A,B相互独立.
(1)乙恰好摸到一个红球包括两种情况,甲第一次摸到一个红球,第二次没有摸到红球改为乙摸球,且摸到一个红球;
二是甲第一次摸球,摸到一个白球,乙开始摸球摸到一个红球,乙接着摸球,摸到一个白球.
∴乙恰好摸到一个红球的概率为
P1=P(A••B)+P(•B•)=××+××=(2)甲至少摸到一个红球的对立事件是甲在前三次摸球中没有摸到红球
∵甲在前三次摸球中,没有摸到红球的概率为
P=P(•B)+P(••)=×+()3=,
根据对立事件的概率公式得到
甲至少摸到一个红球的概率为
P2=1-P=1-=(3)甲摸到红球的次数为ξ,根据题意知ξ的可能取值为0,1,2,3,
结合变量对应的事件写出变量的分布列,
P(ξ=0)=P(•B)+P(••)=×+()3=,
P(ξ=1)=P(A•)+P(••A)=×+()2×=,
P(ξ=2)=P(A•A•)=()2×=,
P(ξ=3)=P(A•A•A)=()3=.
∴ξ的分布列为
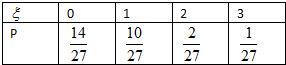
∴数学期望
Eξ=0×+1×+2×+3×=.
点评:本题考查离散型随机变量的分布列和期望,考查相互独立事件同时发生的概率,是一个综合题,解题时注意离散型随机变量对应的事件.




 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案