
【题目】工厂需要围建一个面积为512![]() 的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁.我们知道,砌起的新墙的总长度
的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁.我们知道,砌起的新墙的总长度![]() (单位:
(单位: ![]() )是利用原有墙壁长度
)是利用原有墙壁长度![]() (单位:
(单位: ![]() )的函数.
)的函数.
(1)写出![]() 关于
关于![]() 的函数解析式,确定
的函数解析式,确定![]() 的取值范围.
的取值范围.
(2)堆料场的长、宽之比为多少时,需要砌起的新墙用的材料最省?
【答案】(1) ![]() =
= ![]() +
+![]() ,
, ![]() ;(2) 堆料场的长:宽=2:1时,需要砌的墙所用材料最省.
;(2) 堆料场的长:宽=2:1时,需要砌的墙所用材料最省.
【解析】试题分析:(1)利用矩形堆料场的面积512![]() 和利用原有墙壁长度
和利用原有墙壁长度![]() 可求得矩形堆料场的另一边新墙的长度为
可求得矩形堆料场的另一边新墙的长度为![]() ,所以砌起的新墙的总长度为
,所以砌起的新墙的总长度为![]() ; (2)求砌起的新墙用的材料最省,就是求函数
; (2)求砌起的新墙用的材料最省,就是求函数![]() 的最小值,求函数
的最小值,求函数![]() 的导数,解不等式
的导数,解不等式![]() 和
和![]() ,可得单调性:当
,可得单调性:当![]() ,
, ![]() 随着
随着![]() 的增大而减小,当
的增大而减小,当![]() 时,
时, ![]() 随着
随着![]() 的增大而增大.所以
的增大而增大.所以![]() 时,
时, ![]() 此时,宽为
此时,宽为![]() ,求得长:宽=32:16=2:1,可得结论。
,求得长:宽=32:16=2:1,可得结论。
试题解析:(1)![]() =
= ![]() +
+![]() ,
, ![]() ;
;
由题意知,矩形堆料场利用原有的墙壁的边长为![]() ,另一边为
,另一边为![]() ,则砌起的总长度
,则砌起的总长度
![]() =
= ![]() +
+![]() ,
, ![]() ;
;
(2) ![]() ,令
,令![]() 得
得![]() (
(![]() 舍去)
舍去)
当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
故当![]() ,
, ![]() 随着
随着![]() 的增大而减小,当
的增大而减小,当![]() 时,
时, ![]() 随着
随着![]() 的增大而增大. 由以上可知,当长
的增大而增大. 由以上可知,当长![]() ,宽
,宽![]() 时,
时, ![]() 所以堆料场的长:宽=2:1时,需要砌的墙所用材料最省.
所以堆料场的长:宽=2:1时,需要砌的墙所用材料最省.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,PA、PC切⊙O于A、C,PBD为⊙O的割线. 
(1)求证:ADBC=ABDC;
(2)已知PB=2,PA=3,求△ABC与△ACD的面积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数是数学中重要的概念之一,同学们在初三、高一分别学习过,也知晓其发展过程.1692年,德国数学家莱布尼茨首次使用function这个词,1734年瑞士数学家欧拉首次使用符号f(x)表示函数.1859年我国清代数学家李善兰将function译作函数,“函”意味着信件,巧妙地揭示了对应关系.密码学中的加密和解密其实就是函数与反函数.对自变量恰当地赋值是处理函数问题,尤其是处理抽象函数问题的常用方法之一.请你解答下列问题.
已知函数f(x)满足:对任意的整数a,b均有f(a+b)=f(a) +f(b)+ab+2,且f(-2)=-3.求f(96)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下命题:
①“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
②命题“若 ![]() ,则
,则 ![]() ”的逆否命题为“若
”的逆否命题为“若 ![]() ,则
,则 ![]() ”;
”;
③对于命题 ![]() :
: ![]() ,使得
,使得 ![]() ,则
,则 ![]() :
: ![]() ,均有
,均有 ![]() ;
;
④若 “![]() 为假命题,则
为假命题,则 ![]() ,
, ![]() 均为假命题;
均为假命题;
其中正确命题的序号为_______________(把所有正确命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)若函数![]() 的图象上的所有点的横坐标伸长到原来的
的图象上的所有点的横坐标伸长到原来的![]() 倍,所得的图象与直线
倍,所得的图象与直线![]() 交点的横坐标由小到大依次是
交点的横坐标由小到大依次是![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 为平行四边形ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD
为平行四边形ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD![]() 平面PBC=
平面PBC=![]() .
.
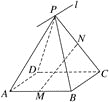
(1)求证:BC∥![]() ;
;
(2)MN与平面PAD是否平行?试证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com