
【题目】下列说法正确的是( )
A. 命题“若x2=1,则x=1”的否命题是“若x2=1,则x≠1”
B. 若命题p:x0∈R,![]() ,则
,则![]() :x∈R,x2-2x-1<0
:x∈R,x2-2x-1<0
C. 命题“若x=y,则sin x=sin y”的逆否命题为真命题
D. “x=-1”是“x2-5x-6=0”的必要不充分条件
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知命题p:(x-2)(x+m)≤0,q:x2+(1-m)x-m≤0.
(1)若m=3,命题“p∧q”为真命题,求实数x的取值范围.
(2)若p是q的必要不充分条件,求实数m的取范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某气象站观测点记录的连续4天里,AQI指数M与当天的空气水平可见度y(单位cm)的情况如下表1:
M | 900 | 700 | 300 | 100 |
y | 0.5 | 3.5 | 6.5 | 9.5 |
哈尔滨市某月AQI指数频数分布如下表2:
M | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设x= ![]() ,根据表1的数据,求出y关于x的回归方程; (参考公式:
,根据表1的数据,求出y关于x的回归方程; (参考公式: ![]() ;其中
;其中 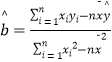 ,
, ![]() )
)
(2)小张开了一家洗车店,经统计,当M不高于200时,洗车店平均每天亏损约2000元;当M在200至400时,洗车店平均每天收入约4000元;当M大于400时,洗车店平均每天收入约7000元;根据表2估计小张的洗车店该月份平均每天的收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在圆心角为![]() ,半径为
,半径为![]() 的扇形铁皮上截取一块矩形材料
的扇形铁皮上截取一块矩形材料![]() ,其中点
,其中点![]() 为圆心,点
为圆心,点![]() 在圆弧上,点
在圆弧上,点![]() 在两半径上,现将此矩形铁皮
在两半径上,现将此矩形铁皮![]() 卷成一个以
卷成一个以![]() 为母线的圆柱形铁皮罐的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形铁皮罐的侧面(不计剪裁和拼接损耗),设矩形的边长![]() ,圆柱形铁皮罐的容积为
,圆柱形铁皮罐的容积为![]() .
.

(1)求圆柱形铁皮罐的容积![]() 关于
关于![]() 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)当![]() 为何值时,才使做出的圆柱形铁皮罐的容积
为何值时,才使做出的圆柱形铁皮罐的容积![]() 最大?最大容积是多少? (圆柱体积公式:
最大?最大容积是多少? (圆柱体积公式:![]() ,
,![]() 为圆柱的底面枳,
为圆柱的底面枳,![]() 为圆柱的高)
为圆柱的高)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F. 
(1)求证:DE是圆O的切线;
(2)若∠CAB=60°,⊙O的半径为2,EC=1,求DE的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最小值为60°;
其中正确的是(填写所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位员工![]() 人参加“学雷锋”志愿活动,按年龄分组:第
人参加“学雷锋”志愿活动,按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
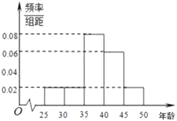
(1)下表是年龄的频率分布表,求正整数![]() 的值;
的值;
区间 |
|
|
|
|
|
人数 |
|
|
|
|
|
(2)现在要从年龄较小的第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,年龄在第
人,年龄在第![]() 组抽取的员工的人数分别是多少?
组抽取的员工的人数分别是多少?
(3)在(2)的前提下,从这![]() 人中随机抽取
人中随机抽取![]() 人参加社区宣传交流活动,求至少有
人参加社区宣传交流活动,求至少有![]() 人年龄在第
人年龄在第![]() 组的概率.
组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,以x轴非负半轴为极轴,与直角坐标系xOy取相同的长度单位,建立极坐标系.设曲线C的参数方程为![]() (θ为参数),直线l的极坐标方程为ρcos
(θ为参数),直线l的极坐标方程为ρcos![]() =2
=2![]() .
.
(1)写出曲线C的普通方程和直线l的直角坐标方程;
(2)求曲线C上的点到直线l的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在对学生的综合素质评价中,将其测评结果分为“优秀、合格、不合格”三个等级,其中不小于80分为“优秀”,小于60分为“不合格”,其它为“合格”. 参考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
(1)某校高一年级有男生500人,女生400人,为了解性别对该综合素质评价结果的影响,采用分层抽样的方法从高一学生中抽取45名学生的综合素质评价结果,其各个等级的频数统计如下表:
等级 | 优秀 | 合格 | 不合格 |
男生(人) | 15 | x | 5 |
女生(人) | 15 | 3 | y |
根据表中统计的数据填写下面2×2列联表,并判断是否有90%的把握认为“综合素质评价测评结果为优秀与性别有关”?
优秀 | 男生 | 女生 | 总计 |
非优秀 | |||
总计 |
(2)以(1)中抽取的45名学生的综合素质评价等级的频率作为全市各个评价等级发生的概率,且每名学生是否“优秀”相互独立,现从该市高一学生中随机抽取3人. ①求所选3人中恰有2人综合素质评价为“优秀”的概率;
②记X表示这3人中综合素质评价等级为“优秀”的个数,求X的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com